题目内容
下面有4个正整数的集合:
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
考点:算术平均数
专题:
分析:分别列出符合(1)、(2)、(3)、(4)条件的正整数集合,然后分别求出它们的平均数,最后比较一下,找出平均数最大的集合.
解答:解:∵每一个正整数集合中所包含的数的平均数是第一个数与最后一个数的和的一半,
∴(1)1~97中3的倍数的正整数集合是{3、6、9、12…96}的平均数是(3+96)÷2=49.5,
(2)1~97中4的倍数的正整数集合是{4、8、12、16…96}的平均数是(4+96)÷2=50,
(3)1~97中5的倍数的正整数集合是{5、10、15、20…95}的平均数是(5+95)÷2=50,
(4)l~97中6的倍数的正整数集合是{6、12、18、24…96}的平均数是(6+96)÷2=51,
其中平均数最大的集合是(4);
故选C.
∴(1)1~97中3的倍数的正整数集合是{3、6、9、12…96}的平均数是(3+96)÷2=49.5,
(2)1~97中4的倍数的正整数集合是{4、8、12、16…96}的平均数是(4+96)÷2=50,
(3)1~97中5的倍数的正整数集合是{5、10、15、20…95}的平均数是(5+95)÷2=50,
(4)l~97中6的倍数的正整数集合是{6、12、18、24…96}的平均数是(6+96)÷2=51,
其中平均数最大的集合是(4);
故选C.
点评:此题考查了算术平均数,解答此题的难点是找出每一个正整数集合的平均数的计算公式.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知二次函数y=-2(x+1)2+4,则( )
| A、其图象的开口向上 |
| B、其图象的对称轴为直线x=1 |
| C、其最大值为4 |
| D、当x<-1时,y随x的增大而减少 |
 已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )| A、x>-2 | B、x<-2 |
| C、x>2 | D、x<3 |
随着我市的经济迅猛发展,连云港港口货物吞吐量逐年增长,2013年全年港口货物吞吐量达800万吨.其中“800万”用科学记数法可表示为( )
| A、0.8×107 |
| B、8×107 |
| C、8×106 |
| D、80×106 |
 图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=
图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=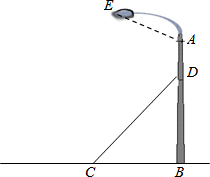 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.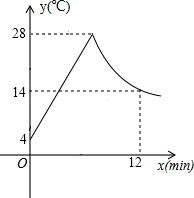 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.