题目内容
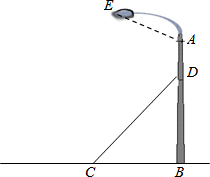 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.(1)求钢缆CD的长度;
(2)若AD=2.1米,灯的顶端E距离A处1.8米,且∠EAB=120°,则灯的顶端E距离地面多少米?(参考数据:sing37°≈0.60,cos37°≈0.80,tan37°≈0.75)
考点:解直角三角形的应用
专题:
分析:(1)根据三角函数可求得CD;
(2)过点E作EF⊥AB于点F.由∠EAB=120°,得∠EAF=60°,再根据三角函数求得AF,从而得出答案.
(2)过点E作EF⊥AB于点F.由∠EAB=120°,得∠EAF=60°,再根据三角函数求得AF,从而得出答案.
解答:解:(1)在Rt△DCB中,sin∠DCB=
=0.6,
∴设DB=3x,DC=5x,
∴(3x)2+16=(5x)2,
解得x=±1(负值舍去),
∴ CD=5米,DB=3米.
CD=5米,DB=3米.
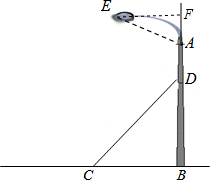
(2)如图,过点E作EF⊥AB于点F.
∵∠EAB=120°,
∴∠EAF=60°,
∴AF=AE•cos∠EAF=1.8×
=0.9(米),
∴FB=AF+AD+DB=0.9+2.1+3=6(米).
∴灯的顶端E距离地面6米.
| DB |
| DC |
∴设DB=3x,DC=5x,
∴(3x)2+16=(5x)2,
解得x=±1(负值舍去),
∴
 CD=5米,DB=3米.
CD=5米,DB=3米.(2)如图,过点E作EF⊥AB于点F.
∵∠EAB=120°,
∴∠EAF=60°,
∴AF=AE•cos∠EAF=1.8×
| 1 |
| 2 |
∴FB=AF+AD+DB=0.9+2.1+3=6(米).
∴灯的顶端E距离地面6米.
点评:本题考查了解直角三角形的应用,运用三角函数可得出答案.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
关于函数y=
x2+(3-
)x+1-
(a≠0),给出下列结论:
①当a=2时,该函数的顶点坐标为(-
,-
)
②当a≠0时,该函数图象经过同一点;
③当a<0时,函数图象截x轴所得线段长度大于
;
④当a>0时,函数在x>
时,y随x的增大而增大.
其中正确的结论有( )
| 3 |
| a |
| 2 |
| a |
| 1 |
| a |
①当a=2时,该函数的顶点坐标为(-
| 2 |
| 3 |
| 1 |
| 6 |
②当a≠0时,该函数图象经过同一点;
③当a<0时,函数图象截x轴所得线段长度大于
| 4 |
| 3 |
④当a>0时,函数在x>
| 1 |
| 3 |
其中正确的结论有( )
| A、①②④ | B、②③④ |
| C、①③ | D、①②③④ |
下面哪个数的倒数是-
( )
| 1 |
| 5 |
A、
| ||
| B、-5 | ||
C、-
| ||
| D、5 |
下面有4个正整数的集合:
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
 如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.