题目内容
已知:关于x的函数y=kx2+k2x-2的图象与y轴交于点C,
(1)当k=-2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若k≥1时函数y随着x的增大而减小,求k的取值范围.
(1)当k=-2时,求图象与x轴的公共点个数;
(2)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
(3)若k≥1时函数y随着x的增大而减小,求k的取值范围.
考点:抛物线与x轴的交点,等腰三角形的性质
专题:
分析:(1)△=b2-4ac=0时,抛物线与x轴有1个交点(或者把k=2代入函数关系,直接求得抛物线与x轴的交点横坐标);
(2)根据△AOC是等腰直角三角形易求点A的坐标为(2,0)或(-2,0).把点A的坐标代入函数解析式,通过方程来求k的值;
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下.则k<0,且对称轴在直线x=1的左侧,故-
≤1,即-
≤1.
(2)根据△AOC是等腰直角三角形易求点A的坐标为(2,0)或(-2,0).把点A的坐标代入函数解析式,通过方程来求k的值;
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下.则k<0,且对称轴在直线x=1的左侧,故-
| k2 |
| 2k |
| k |
| 2 |
解答:解 (1)方法一:当k=-2时,函数为y=-2x2+4x-2,
∵b2-4ac=42-4×(-2)×(-2)=0
∴图象与x轴公共点只有一个.
方法二:当k=-2时,函数为y=-2x2+4x-2,
令y=0,则-2x2+4x-2=0,
解得:x1=x2=1,
∴图象与x轴公共点只有一个;
(2)当△AOC是等腰三角形时,
∵∠AOC=90°,OC=2,
∴可得OA=OC=2
∴点A的坐标为(2,0)或(-2,0).
把x=2,y=0代入解析式 得2k2+4k-2=0,
解得 k1=-1+
,k1=-1-
,
把x=-2,y=0代入解析式 得-2k2+4k-2=0,
解得 k1=-k1=1.
∴k的值为-1+
或-1-
或1;
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下,
∴k<0,且对称轴在直线x=1的左侧,
∴-
≤1,即-
≤1.
解不等式组
,
解得-2≤k<0.
∵b2-4ac=42-4×(-2)×(-2)=0
∴图象与x轴公共点只有一个.
方法二:当k=-2时,函数为y=-2x2+4x-2,
令y=0,则-2x2+4x-2=0,
解得:x1=x2=1,
∴图象与x轴公共点只有一个;
(2)当△AOC是等腰三角形时,
∵∠AOC=90°,OC=2,
∴可得OA=OC=2
∴点A的坐标为(2,0)或(-2,0).
把x=2,y=0代入解析式 得2k2+4k-2=0,
解得 k1=-1+
| 2 |
| 2 |
把x=-2,y=0代入解析式 得-2k2+4k-2=0,
解得 k1=-k1=1.
∴k的值为-1+
| 2 |
| 2 |
(3)由“k≥1时函数y随着x的增大而减小”可知,抛物线开口向下,
∴k<0,且对称轴在直线x=1的左侧,
∴-
| k2 |
| 2k |
| k |
| 2 |
解不等式组
|
解得-2≤k<0.
点评:本题考查了抛物线与x轴的交点,等腰三角形的性质.熟悉判别式和二次函数与x轴交点的关系是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
2014年2月我国出口1141亿美元,进口1370.8亿美元,贸易逆差229.8亿美元,用科学记数法表示-229.8亿美元(保留3个有效数字)( )
| A、-2.29×1010 |
| B、-2.30×1010 |
| C、-2.3×109 |
| D、-2.30×109 |
下面有4个正整数的集合:
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
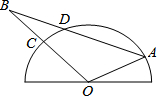 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为 如图,一次函数y=-
如图,一次函数y=-