题目内容
已知一次函数y=kx+b的图象如图，则关于x的不等式k（x-4）-2b＞0的解集为（ ）| A、x＞-2 | B、x＜-2 |
| C、x＞2 | D、x＜3 |
考点：一次函数与一元一次不等式
专题：
分析：根据函数图象知：一次函数过点（3，0）；将此点坐标代入一次函数的解析式中，可求出k、b的关系式；然后将k、b的关系式代入k（x-4）-2b＞0中进行求解．
解答：解：∵一次函数y=kx+b经过点（3，0），
∴3k+b=0，
∴b=-3k．
将b=-3k代入k（x-4）-2b＞0，
得k（x-4）-2×（-3k）＞0，
去括号得：kx-4k+6k＞0，
移项、合并同类项得：kx＞-2k；
∵函数值y随x的增大而减小，
∴k＜0；
将不等式两边同时除以k，得x＜-2．
故选B．
∴3k+b=0，
∴b=-3k．
将b=-3k代入k（x-4）-2b＞0，
得k（x-4）-2×（-3k）＞0，
去括号得：kx-4k+6k＞0，
移项、合并同类项得：kx＞-2k；
∵函数值y随x的增大而减小，
∴k＜0；
将不等式两边同时除以k，得x＜-2．
故选B．
点评：本题考查了一次函数与不等式的关系及数形结合思想的应用．解决此类问题关键是仔细观察图形，注意几个关键点（交点、原点等），做到数形结合．
练习册系列答案
相关题目
当m＜-1时，方程（m3+1）x2+（m2+1）x=m+1的根的情况是（ ）
| A、两负根 |
| B、两异号根，且正根的绝对值较大 |
| C、两正根 |
| D、两异号根，且负根的绝对值较大 |
关于函数y=
x2+（3-
）x+1-
（a≠0），给出下列结论：
①当a=2时，该函数的顶点坐标为（-
，-
）
②当a≠0时，该函数图象经过同一点；
③当a＜0时，函数图象截x轴所得线段长度大于
；
④当a＞0时，函数在x＞
时，y随x的增大而增大．
其中正确的结论有（ ）
| 3 |
| a |
| 2 |
| a |
| 1 |
| a |
①当a=2时，该函数的顶点坐标为（-
| 2 |
| 3 |
| 1 |
| 6 |
②当a≠0时，该函数图象经过同一点；
③当a＜0时，函数图象截x轴所得线段长度大于
| 4 |
| 3 |
④当a＞0时，函数在x＞
| 1 |
| 3 |
其中正确的结论有（ ）
| A、①②④ | B、②③④ |
| C、①③ | D、①②③④ |
2014年2月我国出口1141亿美元，进口1370.8亿美元，贸易逆差229.8亿美元，用科学记数法表示-229.8亿美元（保留3个有效数字）（ ）
| A、-2.29×1010 |
| B、-2.30×1010 |
| C、-2.3×109 |
| D、-2.30×109 |
下面哪个数的倒数是-
（ ）
| 1 |
| 5 |
A、
| ||
| B、-5 | ||
C、-
| ||
| D、5 |
下面有4个正整数的集合：
（1）1～97中3的倍数；
（2）1～97中4的倍数；
（3）1～97中5的倍数；
（4）l～97中6的倍数．
其中平均数最大的集合是（ ）
（1）1～97中3的倍数；
（2）1～97中4的倍数；
（3）1～97中5的倍数；
（4）l～97中6的倍数．
其中平均数最大的集合是（ ）
| A、（1） | B、（2） |
| C、（3） | D、（4） |
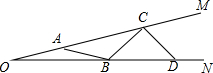如图，在∠MON的两边依次截取OA=AB=BC=CD=2．