题目内容
 图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=
图中S□ABCD=18cm2,P为BC边上任意一点,M为AP上的一个点,且AM=| 1 |
| 2 |
考点:平行四边形的性质
专题:
分析:由S□ABCD=18cm2,可求得△APD的面积,又由AM=
MP,根据等高三角形的面积比等于对应底的比,即可求得答案.
| 1 |
| 2 |
解答:解:∵S□ABCD=18cm2,
∴S△ADP=
S□ABCD=9cm2,
∵AM=
MP,
∴MP=
AP,
∴S△PDM=
S△APD=
×9=6(cm2).
故答案为:6.
∴S△ADP=
| 1 |
| 2 |
∵AM=
| 1 |
| 2 |
∴MP=
| 2 |
| 3 |
∴S△PDM=
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:6.
点评:此题考查了平行四边形的性质.此题难度不大,注意掌握等高三角形的面积比等于对应底的比.

练习册系列答案
相关题目
当m<-1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是( )
| A、两负根 |
| B、两异号根,且正根的绝对值较大 |
| C、两正根 |
| D、两异号根,且负根的绝对值较大 |
下面有4个正整数的集合:
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
(1)1~97中3的倍数;
(2)1~97中4的倍数;
(3)1~97中5的倍数;
(4)l~97中6的倍数.
其中平均数最大的集合是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
 某校一周中五天的用水量如图,则该校这五天的平均用水量是
某校一周中五天的用水量如图,则该校这五天的平均用水量是 如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C=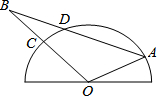 如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为
如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,∠B的度数为