题目内容
18.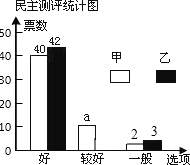 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:五位评委的打分表
| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
分析 (1)利用中位数及平均数的定义分别求解即可;
(2)用样本个数减去其他小组的频数即可求得a值,从而补全统计图;
(3)分别根据打分要求确定两人的成绩,然后即可确定参选人员.
解答  解:(1)${\bar x_乙}=\frac{88+87+90+98+92}{5}=91$(分);
解:(1)${\bar x_乙}=\frac{88+87+90+98+92}{5}=91$(分);
中位数是90分.
(2)a=50-40-2=8,
如图1即为所求;
(3)①甲的才艺分=$\frac{89+91+93}{3}=91$(分),
甲的测评分=40×2+8×1+2×0=88(分),
甲的综合分=91×0.6+88×(1-0.6)=89.8(分),
乙的才艺分=$\frac{88+90+92}{3}=90$(分),
乙的测评分=42×2+5×1+2×0=89(分),
乙的综合分=90×0.6+89×(1-0.6)=89.6(分),
∵甲的综合分>乙的综合分,
∴应选拔甲同学去参加艺术节演出.
②甲的综合分=91k+(40×2+8×1+2×0)×(1-k)=3k+88,
乙的综合分=90k+(42×2+5×1+2×0)×(1-k)=k+89,
若从甲、乙二人中只选拔出一人去参加演出,
则 3k+88≠k+89,
∴k≠0.5.
点评 本题考查了中位数、加权平均数及条形统计图的知识,解题的关键是能够读懂题意,并能正确的识图,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )
 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
3.事件“反比例函数y=$\frac{k}{x}$(k>0)经过点(0,3)”的概率是( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{k}$ | D. | 1 |
7.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | B. | 垂线段最短 | ||
| C. | $\sqrt{81}$的平方根是±9 | D. | 无限小数都是无理数 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )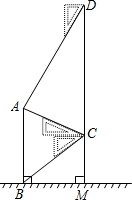 如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB.为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角为30°,底部点B的俯角为45°,小华在五楼找到一点D,利用三角尺测得点A的俯角为60°.若CD为9.6m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73). 如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,
如图,直线y=kx过点A(1,2),直线y=-2x-5与x轴交于B点,直线y=kx与直线y=-2x-5交于C点,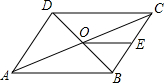 如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.
如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.