题目内容
14. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.(1)求证:点E是边BC的中点;
(2)当∠B=45°时,四边形ODEC是正方形.
分析 (1)利用EC为⊙O的切线,ED也为⊙O的切线可求EC=ED,再求得EB=EC,EB=ED可知点E是边BC的中点;
(2)当∠B=45°时,四边形ODEC是正方形,由等腰三角形的性质,得到∠ODA=∠A=45°,于是∠DOC=90°然后根据有一组邻边相等的矩形是正方形,即可得到结论.
解答 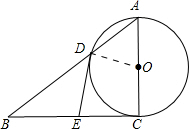 解:(1)证明:连接DO;
解:(1)证明:连接DO;
∵∠ACB=90°,AC为直径,
∴EC为⊙O的切线;
又∵ED也为⊙O的切线,
∴EC=ED,
又∵∠EDO=90°,
∴∠BDE+∠ADO=90°,
∴∠BDE+∠A=90°
又∵∠B+∠A=90°,
∴∠BDE=∠B,
∴EB=ED,
∴EB=EC,即点E是边BC的中点;
(2)当∠B=45°时,四边形ODEC是正方形,
∵∠ACB=90°,
∴∠A=45°,
∵OA=OD,
∴∠ADO=45°,
∴∠AOD=90°,
∴∠DOC=90°,
∵∠ODE=90°,
∴四边形DECO是矩形,
∵OD=OC,
∴矩形DECO是正方形.
故答案为:45°.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
5.下列判断不正确的是( )
| A. | 四个角相等的四边形是矩形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的平行四边形是矩形 | D. | 对角线垂直的平行四边形是菱形 |
9.若$\sqrt{2x-3}$是二次根式,则x应满足的条件是( )
| A. | x>$\frac{3}{2}$ | B. | x≥$\frac{3}{2}$ | C. | x<$\frac{3}{2}$ | D. | x≤$\frac{3}{2}$ |
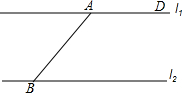 如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.