题目内容
8. 如图,正方形ABCD中,E、F两点分别在BC、CD上,BE+DF=EF.求证:
如图,正方形ABCD中,E、F两点分别在BC、CD上,BE+DF=EF.求证:(1)∠EAF=45°;
(2)FA平分∠DFE.
分析 (1)延长CB至G,使BG=FD,连接AG,如图1,利用“SAS”证明△ABG≌△ADF,得到AG=AF,∠BAG=∠DAF,而EF=BE+DF,所以EF=EG,再根据“SSS”证明△AEG≌△AEF,得到∠EAG=∠EAF,则∠EAF=∠DAF+∠ABE,然后利用∠EAF+∠DAF+∠ABE=90°,即可得到∠EAF=45°;
(2)根据全等三角形的性质得到∠G=∠AFD,∠G=∠AFE,等量代换得到∠AFE=∠AFD,即可得到结论.
解答 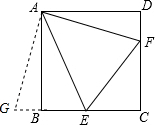 证明:(1)延长CB至G,使BG=FD,连接AG,如图,
证明:(1)延长CB至G,使BG=FD,连接AG,如图,
∵四边形ABCD为正方形,
∴AB=AD,∠ABC=∠D=90°,
在△ABG和△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{∠ABG=∠D}\\{BG=DF}\end{array}\right.$,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠BAG=∠DAF,
∵EF=BE+DF,
∴EF=EG,
在△AEG和△AEF中,
$\left\{\begin{array}{l}{AE=AE}\\{AG=AF}\\{GE=EF}\end{array}\right.$,
∴△AEG≌△AEF(SSS),
∴∠EAG=∠EAF,
∵∠BAG=∠DAF,
∴∠EAF=∠DAF+∠ABE,
∵∠EAF+∠DAF+∠ABE=90°,
∴∠EAF=45°;
(2)∵△ABG≌△ADF,
∴∠G=∠AFD,
∵△AEG≌△AEF,
∴∠G=∠AFE,
∴∠AFE=∠AFD,
∴FA平分∠DFE.
点评 本题考查了全等三角形的判定和性质,正方形的性质,角平分线的定义,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图所示,一块儿三角形空地ABC,要在其内部建一个菱形花园,使得B为菱形花园的一个顶点,其余3个顶点分别在△ABC的3条边上.你能设计出此菱形花园吗?
如图所示,一块儿三角形空地ABC,要在其内部建一个菱形花园,使得B为菱形花园的一个顶点,其余3个顶点分别在△ABC的3条边上.你能设计出此菱形花园吗?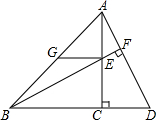 已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
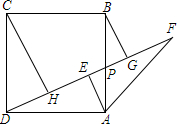 如图,在正方形ABCD中,P为AB边上任意一点,连接DP,过点C作CH⊥DP于点H.过点A作AE⊥DP于点E,延长DP至点F使EF=DE,在HF上取一点G使HG=CH,连接AF、BG.
如图,在正方形ABCD中,P为AB边上任意一点,连接DP,过点C作CH⊥DP于点H.过点A作AE⊥DP于点E,延长DP至点F使EF=DE,在HF上取一点G使HG=CH,连接AF、BG.