题目内容
18.已知0M平分∠A0B,ON平分∠COD,∠BOC=20°,∠AOD=130°,求∠MON的度数.分析 根据题意求出∠COD+∠AOB,根据角平分线的定义得到∠COM+∠BOM=$\frac{1}{2}$(∠COD+∠AOB),结合图形计算即可.
解答 解:∵ ∠BOC=20°,∠AOD=130°,
∠BOC=20°,∠AOD=130°,
∴∠COD+∠AOB=110°,
∵OM平分∠AOB,ON平分∠COD,
∴∠COM=$\frac{1}{2}∠$COD,∠BOM=$\frac{1}{2}$∠AOB,
∴∠COM+∠BOM=$\frac{1}{2}$(∠COD+∠AOB)=55°,
∴∠MON=∠COM+∠BOM+∠BOC=75°.
点评 本题考查的是角平分线的定义,若OC是∠AOB的平分线则∠AOC=∠BOC=$\frac{1}{2}$∠AOB或∠AOB=2∠AOC=2∠BOC.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
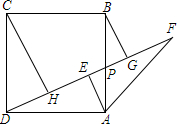 如图,在正方形ABCD中,P为AB边上任意一点,连接DP,过点C作CH⊥DP于点H.过点A作AE⊥DP于点E,延长DP至点F使EF=DE,在HF上取一点G使HG=CH,连接AF、BG.
如图,在正方形ABCD中,P为AB边上任意一点,连接DP,过点C作CH⊥DP于点H.过点A作AE⊥DP于点E,延长DP至点F使EF=DE,在HF上取一点G使HG=CH,连接AF、BG.