题目内容
1.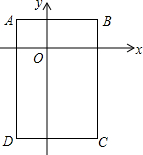 如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$)
如图,长方形ABCD的边与坐标轴平行,点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$)(1)求点B、D的坐标;
(2)一动点P从点A出发,沿长方形的边AB、BC运动至点C停止,运动速度为每秒$\sqrt{3}$个单位,设运动时间为ts.
①当t=1s时,求点P的坐标;
②当t=3s时,求△PDC的面积.
分析 (1)由于长方形ABCD的边与坐标轴平行,则点B的横坐标与点C的横坐标相同,点B的纵坐标与点A的纵坐标相同,这样可得到B点坐标,同样方法可得到D点坐标;
(2)①当t=1s时,AP=$\sqrt{3}$,然后计算出点P到y轴的距离即可得到P点坐标;
②当t=3s时,如图,先计算出PC=2,然后根据三角形面积公式计算.
解答 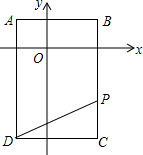 解:(1)∵长方形ABCD的边与坐标轴平行,
解:(1)∵长方形ABCD的边与坐标轴平行,
而点A、C的坐标分别为(-1,1),($\sqrt{3}$,-2$\sqrt{3}$),
∴B($\sqrt{3}$,1),D(-1,-2$\sqrt{3}$);
(2)AB=$\sqrt{3}$+1,BC=1+2$\sqrt{3}$,
①当t=1s时,点P在AB上,则AP=$\sqrt{3}$,
∴点P到y轴的距离为$\sqrt{3}$-1,
∴P($\sqrt{3}$-1,1);
②当t=3s时,PC=1+2$\sqrt{3}$+1+$\sqrt{3}$-3$\sqrt{3}$=2,
则△PDC的面积=$\frac{1}{2}$CD•PC=$\frac{1}{2}$×(1+$\sqrt{3}$)×2=1+$\sqrt{3}$.
点评 本题考查了坐标与图形性质:利用平行于坐标的直线上点的坐标特征计算相应线段的长.解决本题的关键是利用坐标计算线段的长.

练习册系列答案
相关题目
20.已知抛物线y=x2-2mx+m2+m+2与x轴的交点为(a,0),(b,0),则(a-1)2+(b-1)2的最小值是( )
| A. | 10 | B. | 15 | C. | 18 | D. | 20 |
11.在平面直角坐标系中,点(5,3)关于x轴的对称点是( )
| A. | (3,5) | B. | (5,-3) | C. | (-5,3) | D. | (-5,-3) |

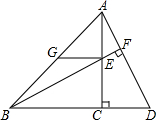 已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.
已知,如图,在等腰Rt△ABC中,∠ACB=90°,点D、E分别在BC延长线及AC上,联结BE并延长交AD于F,过点E作EG∥BC交AB于G,AC=EG+CD.求证:BF⊥AD.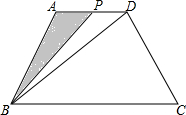 四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.
四边形ABCD中,AD∥BC,AB=CD=5,AD=7,BC=13,S四边形ABCD=40,P是一动点,沿AD,DC由A经D点向C点移动,设P点移动的距离为x.