题目内容
12.下列各式的推论中,不正确的是( )| A. | 由$\frac{a}{b}$=$\frac{c}{d}$,得$\frac{a+c}{b+d}$=$\frac{c}{d}$ | B. | 由$\frac{a}{b}$=$\frac{c}{d}$,得$\frac{ax}{bx}$=$\frac{c}{d}$(x≠0) | ||
| C. | 由$\frac{a}{b}$=$\frac{c}{d}$,得$\frac{a±b}{b}$=$\frac{c±d}{d}$ | D. | 由$\frac{a}{b}$=$\frac{c}{d}$,得$\frac{a±1}{b}$=$\frac{c±1}{d}$ |
分析 A、利用等比性质得出结论;
B、利用比例的基本性质得出结论;
C、利用合分比性质得出结论;
D、分子要加或减分母,才是合分比的性质,所以不正确.
解答 解:A、由$\frac{a}{b}$=$\frac{c}{d}$,根据等比性质得$\frac{a+c}{b+d}$=$\frac{c}{d}$,所以选项A正确;
B、由$\frac{a}{b}$=$\frac{c}{d}$,根据比例的基本性质得$\frac{ax}{bx}$=$\frac{c}{d}$(x≠0),所以选项B正确;
C、由$\frac{a}{b}$=$\frac{c}{d}$,根据合分比性质得$\frac{a±b}{b}$=$\frac{c±d}{d}$,所以选项C正确;
D、根据合分比性质得,选项D不正确;
因为本题选择不正确的,故选D.
点评 本题考查了比例的性质,熟练掌握常用的性质有:①内项之积等于外项之积.若$\frac{a}{b}=\frac{c}{d}$时,则ad=bc.②合比性质:若$\frac{a}{b}=\frac{c}{d}$,则$\frac{a+b}{b}=\frac{c+d}{d}$.③分比性质:若若$\frac{a}{b}=\frac{c}{d}$,则$\frac{a-b}{b}=\frac{c-d}{d}$.④合分比性质.若若$\frac{a}{b}=\frac{c}{d}$,则$\frac{a+b}{a-b}=\frac{c+d}{c-d}$.⑤等比性质.若若$\frac{a}{b}=\frac{c}{d}$=…=$\frac{m}{n}$(b+d+…+n≠0),则$\frac{a+b+…+m}{c+d+…+n}$=$\frac{m}{n}$.

练习册系列答案
相关题目
2.若$\frac{a}{b}$=$\frac{c}{d}$=$\frac{1}{2}$,(b-2d≠0),则$\frac{a-2c}{b-2d}$=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
20.一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来的方向相同,这两次拐弯的角度可能是( )
| A. | 第一次向右拐40°,第二次向左拐140° | |
| B. | 第一次向右拐40°,第二次向右拐140° | |
| C. | 第一次向左拐40°,第二次向左拐140° | |
| D. | 第一次向左拐40°,第二次向右拐40° |
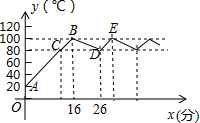 张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.
张老师办公室的饮水机具有自动调节功能,开机后自动进行加热状态,水温y(℃)与开机后用时x(分钟)成一次函数关系,当水温上升到100℃时停止加热,水温开始下降,此时水温y(℃)与开机后用时x(分钟)仍成一次函数某天早晨7:00时,张老师打开饮水机,水温变化情况如图所示.