题目内容
已知不等式mx-3＞2x+m．
（1）若它的解集是x＜
，求m的取值范围；
（2）若它的解集与不等式2x-1＞3-x的解集相同，求m的值．
（1）若它的解集是x＜
| m+3 |
| m-2 |
（2）若它的解集与不等式2x-1＞3-x的解集相同，求m的值．
考点：不等式的解集
专题：
分析：（1）首先移项可得mx-2x＞m+3，合并同类项可得（m-2）x＞m+3，再两边同时除以m-2，当m-2＞0时，可得x＜
；
（2）首先解不等式2x-1＞3-x，可得解集，再解（m-2）x＞m+3，再两边同时除以m-2，当m-2＞0时，可得x＞
，进而得到方程
=
，再解方程即可．
| m+3 |
| m-2 |
（2）首先解不等式2x-1＞3-x，可得解集，再解（m-2）x＞m+3，再两边同时除以m-2，当m-2＞0时，可得x＞
| m+3 |
| m-2 |
| m+3 |
| m-2 |
| 3 |
| 4 |
解答：解：mx-3＞2x+m，
mx-2x＞m+3，
（m-2）x＞m+3，
（1）∵它的解集是x＜
，
∴m-2＜0，
解得m＜2；
（2）2x-1＞3-x，
解得：x＞
，
∵它的解集是x＞
，
∴
=
，且m-2＞0，
解得m=17．
mx-2x＞m+3，
（m-2）x＞m+3，
（1）∵它的解集是x＜
| m+3 |
| m-2 |
∴m-2＜0，
解得m＜2；
（2）2x-1＞3-x，
解得：x＞
| 4 |
| 3 |
∵它的解集是x＞
| m+3 |
| m-2 |
∴
| m+3 |
| m-2 |
| 4 |
| 3 |
解得m=17．
点评：此题主要考查了不等式的解集，关键是要注意分类讨论：m-2＞0或m-2＜0．
练习册系列答案
相关题目
PM3.5是大气中直径小于或等于0.0000035米的颗粒物，将0.0000035用科学记数法表示为（ ）
| A、0.35×10-5 |
| B、0.35×10-6 |
| C、3.5×10-5 |
| D、3.5×10-6 |
如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则下列结论正确的是（ ）| A、∠AED=50° |
| B、∠C=60° |
| C、AD=AE |
| D、BC=2DE |
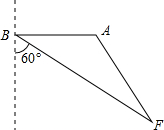由于过度采伐森林和破坏植被，我国许多地区频频遭受沙尘暴的侵袭，今日A市测得沙尘暴中心在A市的正西方向300km的B处，以10
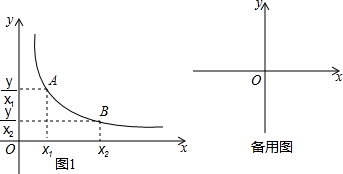[课本节选]