Question

[课本节选]
反比例函数y=

k

x

（k为常数，k≠0）的图象是双曲线，当k＞0时，双曲线两个分支分别在一、三象限，在每一个象限内，随的增大而减小（简称增减性），反比例函数的图象关于原点对称（简称对称性）．
【尝试说理】
我们首先对反比例函数y=

k

x

（k＞0）的增减性来进行说理．
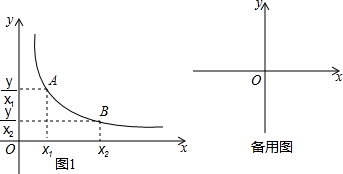
如图，当x＞0时，
在函数图象上如图1任意取两点A、B，设A（x₁，

k

x1

），B（x₂，

k

x2

），且0＜x₁＜x₂．
下面只需要比较

k

x1

和

k

x2

的大小．

k

x1

=

k

x2

-

kx1-x2

x1x2

∵0＜x₁＜x₂，∴x₁-x₂＜0，x₁x₂＞0，面k＞0．
∴

kx1-x2

x 1x2

，即

k

x2

＜

k

x1

．
这说明：x₁＜x₂时，

k

x1

＞

k

x2

．也就是：自变量值增大了，对应的函数值反而变小了．
即：当x＞0时，y随x的增大而减小．
同理：当x＜0时，y随x的增大而减小
（1）试说明：反比例函数y=

k

x

（k＞0）的图象关于原点对称．
【运用推广】
（2）分别写出二次函数y=ax²（a＞0，a常数）的对称性和增减性，并进行说理．
对称性：

 

；增减性：

 

；说理：

 

．
（3）
对于二次函数y=ax²+bx+c（a＞0，a、b、c为常数），请你从增减性的角度，简要解释何当x=-

b

2a

时函数取得最小值．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）设点A（a，b）在函数图象上，将其对称点代入函数解析式也成立，反比例函数y=

k

x

（k＞0）的图象关于原点对称；
（2）设C（c，d），其关于y轴的对称点为C′（-c，d），将两点横坐标代入解析式得到相同的纵坐标，可知其关于y轴对称；取点（x₁，y₁），（x₂，y₂），且x₁＜x₂＜0；则ax₁²＞ax₂²，即y₁＜y₂，可见，y轴左侧，y随x的减小而增大；同理可证，y轴右侧，y随x的增大而增大．
（3）根据对称轴左侧和右侧的坐标对应的函数值都比对称轴对应的函数值大来说理．

解答：解：（1）设点A（a，b）在函数图象上，则有ab=k，
则函数关于原点的对称点为A′（-a，-b），
将A′（-a，-b）代入y=

k

x

有，（-a）（-b）=k，
即ab=k，
可见，A和A′关于原点对称．

（2）关于y轴对称：设C（c，d），其关于y轴的对称点为C′（-c，d），
将C（c，d）代入y=ax²得，d=ac²；将C′（-c，d）代入y=ax²得，d=a（-c）²=ac²．
可见，函数关于y轴对称；
增减性：取点（x₁，y₁），（x₂，y₂），且x₁＜x₂＜0；
则ax₁²＞ax₂²，
即y₁＜y₂，可见，y轴左侧，y随x的减小而增大；同理可证，y轴右侧，y随x的增大而增大．
可见，对称轴左侧和右侧的坐标对应的函数值都比对称轴对应的函数值大，当x=-

b

2a

时函数取得最小值．
故答案为：关于y轴对称；y轴左侧，y随x的减小而增大；y轴右侧，y随x的增大而增大；

（3）关于y轴对称：设C（c，d），其关于y轴的对称点为C′（-c，d），
将C（c，d）代入y=ax²得，d=ac²；将C′（-c，d）代入y=ax²得，d=a（-c）²=ac²．
可见，函数关于y轴对称；
增减性：取点（x₁，y₁），（x₂，y₂），且x₁＜x₂＜0；
则ax₁²＞ax₂²，
即y₁＜y₂，可见，y轴左侧，y随x的减小而增大；同理可证，y轴右侧，y随x的增大而增大．

点评：本题考查了反比例函数综合题，参照例题进行分析和解答是解题的思路，同时要熟悉函数的图象和性质．