题目内容
2．
如图，铁道口拦栏杆的短臂长1.25米，长臂长16.5米，当短臂的端点下降0.85米时，长臂的端点升高了拦栏杆的宽度忽略不计）（ ）| A． | 11米 | B． | 11.22米 | C． | 17米 | D． | 10米 |
分析 首先根据∠DCO=∠ABO=90°，∠AOB=∠COD，可得△CDO∽△BAO，利用该相似三角形的对应边成比例进行解答即可．
解答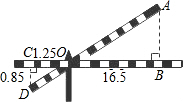 
解：∵∠DCO=∠ABO=90°，∠AOB=∠COD，
∴△CDO∽△BAO，
∴$\frac{CD}{AB}$=$\frac{CO}{BO}$，
∴CO=1.25米，BO=16.5米，DC=0.85米，
∴$\frac{0.85}{AB}$=$\frac{1.25}{16.5}$，解得：AB=11.22，
∴长臂端点升高11.22米．
故选：B．
点评 此题主要考查了相似三角形的应用，关键是掌握相似三角形对应边成比例．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
13．（1）将甲种漆3g与乙种漆4g倒入一容器内搅匀，则甲种漆占混合漆的$\frac{3}{7}$；如从这容器内又倒出5g漆，那么这5㎏漆中有甲种漆有$\frac{15}{7}$g．
（2）小明到姑姑家吃早点时，表妹小红很淘气，她先从一杯豆浆中，取出一勺豆浆，倒入盛牛奶的杯子中搅匀，再从盛牛奶的杯子中取出一勺混合的牛奶和豆浆，倒入盛豆浆的杯子中．小明想：现在两个杯子中都有了牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？（两个杯子原来的牛奶和豆浆一样多）．现在来看小明的分析：
设混合前两个杯子中盛的牛奶和豆浆的体积相等，均为a，一勺的容积为b．为便于理解，将混合前后的体积关系制成下表：
①将上面表格填完（表格中只需列出算式，无需化简）．
②请通过计算判断：最后两个杯子中都有牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？
（2）小明到姑姑家吃早点时，表妹小红很淘气，她先从一杯豆浆中，取出一勺豆浆，倒入盛牛奶的杯子中搅匀，再从盛牛奶的杯子中取出一勺混合的牛奶和豆浆，倒入盛豆浆的杯子中．小明想：现在两个杯子中都有了牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？（两个杯子原来的牛奶和豆浆一样多）．现在来看小明的分析：
设混合前两个杯子中盛的牛奶和豆浆的体积相等，均为a，一勺的容积为b．为便于理解，将混合前后的体积关系制成下表：
| 混合前的体积 | 第一次混合后 | 第二次混合后 | ||||
| 豆浆 | 牛奶 | 豆浆 | 牛奶 | 豆浆 | 牛奶 | |
| 豆浆杯子 | a | 0 | a-b | 0 | a-b+$\frac{{b}^{2}}{a+b}$ | b-$\frac{{b}^{2}}{a+b}$ |
| 牛奶杯子 | 0 | a | b | a | b-$\frac{{b}^{2}}{a+b}$ | a-（b-$\frac{{b}^{2}}{a+b}$） |
②请通过计算判断：最后两个杯子中都有牛奶和豆浆，究竟是豆浆杯子中的牛奶多，还是牛奶杯子中的豆浆多呢？
已知：如图，∠1与∠2互补，∠D=∠B，那么∠A=∠C，请说明理由．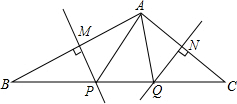
如图，∠BAC=110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是40°．