题目内容
11.求下列各式中的x的值(1)49x2=25
(2)(x+2)2=16
(3)x3-0.027=0
(4)$\frac{1}{2}$(2x-1)3=-4.
分析 (1)先将二次项系数化为1,继而开平方可得出x的值;
(2)开平方可得出x的值;
(3)先移项,然后开立方可得出x的值;
(4)先将二次项系数化为1,然后开立方可得出(2x-1),继而可得出x的值.
解答 解:(1)49x2=25,
x2=$\frac{25}{49}$,
x=±$\frac{5}{7}$;
(2)(x+2)2=16
x+2=±4,
x=-6或x=2;
(3)x3-0.027=0,
x3=0.027,
x=0.3;
(4)$\frac{1}{2}$(2x-1)3=-4,
(2x-1)3=-8,
2x-1=-2,
2x=-1,
x=-$\frac{1}{2}$.
点评 本题考查了平方根及立方根的知识,掌握开平方及开立方的法则是关键.

练习册系列答案
相关题目
2.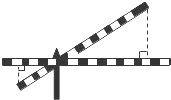 如图,铁道口拦栏杆的短臂长1.25米,长臂长16.5米,当短臂的端点下降0.85米时,长臂的端点升高了拦栏杆的宽度忽略不计)( )
如图,铁道口拦栏杆的短臂长1.25米,长臂长16.5米,当短臂的端点下降0.85米时,长臂的端点升高了拦栏杆的宽度忽略不计)( )
 如图,铁道口拦栏杆的短臂长1.25米,长臂长16.5米,当短臂的端点下降0.85米时,长臂的端点升高了拦栏杆的宽度忽略不计)( )
如图,铁道口拦栏杆的短臂长1.25米,长臂长16.5米,当短臂的端点下降0.85米时,长臂的端点升高了拦栏杆的宽度忽略不计)( )| A. | 11米 | B. | 11.22米 | C. | 17米 | D. | 10米 |
19.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是±$\frac{1}{5}$ | B. | -4是16的一个平方根 | ||
| C. | 0.02的算术平方根是0.0004 | D. | 27的立方根是3 |
6.根据下表回答下列问题:
(1)795.24的算术平方根是28.4;
(2)$\sqrt{823.7}$≈28.7;
(3)$\sqrt{810}$在哪两个数之间?答:在28.4与28.5.
| x | 28.0 | 28.1 | 28.2 | 28.3 | 28.4 | 28.5 | 28.6 | 28.7 | 28.8 |
| x2 | 784.00 | 789.61 | 795.24 | 800.89 | 806.56 | 812.25 | 817.96 | 823.69 | 829.44 |
(2)$\sqrt{823.7}$≈28.7;
(3)$\sqrt{810}$在哪两个数之间?答:在28.4与28.5.
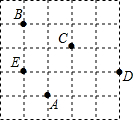 如图所示,如果点A的位置为(-1,-2),那么点B的位置为(-2,1),点C的位置为(0,0),点D(2,-1);点E(-2,-1).
如图所示,如果点A的位置为(-1,-2),那么点B的位置为(-2,1),点C的位置为(0,0),点D(2,-1);点E(-2,-1).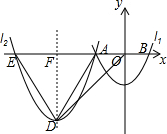 如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y=$\frac{1}{2}$x2-2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=-6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.
如图,在平面直角坐标系中,抛物线l1与x轴交于点A,B,与y轴交于点C,l1的解析式为y=$\frac{1}{2}$x2-2,若将抛物线l1平移,使平移后的抛物线l2经过点A,对称轴为直线x=-6,抛物线l2与x轴的另一个交点是E,顶点是D,连结OD,AD,ED.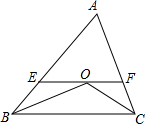 在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.
在△ABC中,AB≠AC,∠ABC和∠ACB的平分线交于点O,过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系.