题目内容
7.(1)计算:$\sqrt{8}+|1-\sqrt{2}|+2sin30°$;(2)解方程:3x2-2x-1=0.
分析 (1)原式第一项化为最简二次根式,第二项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)方程利用因式分解法求出解即可.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$-1+1
=3$\sqrt{2}$;
(2)分解因式得:(3x+1)(x-1)=0,
可得3x+1=0或x-1=0,
解得:x1=-$\frac{1}{3}$,x2=1.
点评 此题考查了实数的运算,以及解一元二次方程-因式分解法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.-3×(-2)=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -6 | D. | $-\frac{1}{6}$ |
16.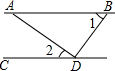 如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
 如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
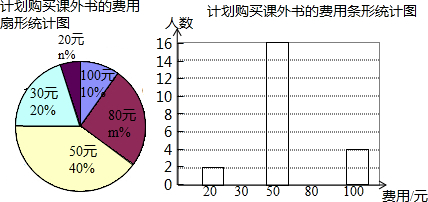
 如图,点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{k}{x}(x>0)$的图象上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB与AD相交于点C,且AC=2CD.
如图,点A(m,3)在反比例函数y=$\frac{3}{x}$(x>0)的图象上,点B在反比例函数y=$\frac{k}{x}(x>0)$的图象上,AB∥x轴,过点A作AD⊥x轴于点D,连接OB与AD相交于点C,且AC=2CD.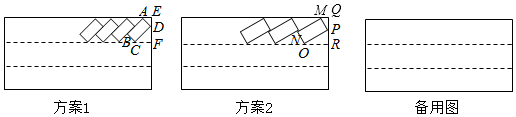
 如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.
如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.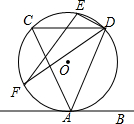 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.