题目内容
19. 如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.
如图,在⊙O中,AB是弦,过点A的切线交BO的延长线于点C,若⊙O的半径为3,∠C=20°,则$\widehat{AB}$的长为$\frac{11}{6}π$.
分析 由AC是⊙O的切线推出OA⊥AC,由∠C=20°,得到∠COA=70°,进而推出圆心角∠AOB=110°,代入弧长公式即可得到结论.
解答 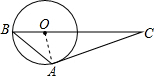 解:连接OA,
解:连接OA,
∵AC是⊙O的切线,
∴OA⊥AC,
∵∠C=20°,
∴∠COA=70°,
∴∠AOB=110°,
∴$\widehat{AB}$的长为$\frac{110π•3}{180}$=$\frac{11}{6}$π.
故答案为$\frac{11}{6}$π.
点评 本题考查了切线的性质,直角三角形的性质,弧长公式,本题关键是求得圆心角∠AOB的度数.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2•4a2=12a2 | C. | (a+2)2=a2+4 | D. | (a+b)(a-b)=a2-b2 |
14.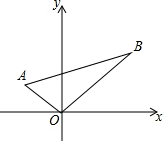 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (2,2) |
 如图,已知a∥b,∠1=65°20′,则∠2=114°40′.
如图,已知a∥b,∠1=65°20′,则∠2=114°40′.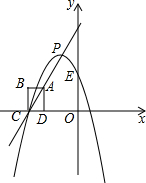 如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.
如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.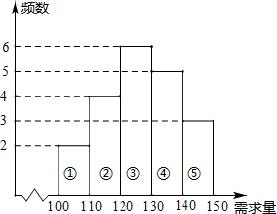 经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.
经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.