题目内容
16.计算:($\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2007}+\sqrt{2008}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2014}}$)(1+$\sqrt{2014}$)分析 先分母有理化,然后合并后利用平方差公式计算.
解答 解:原式=($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2013}}$)•($\sqrt{2014}$+1)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2014}$-$\sqrt{2013}$)($\sqrt{2014}$+1)
=($\sqrt{2014}$-1)($\sqrt{2014}$+1)
=($\sqrt{2014}$)2-12
=2014-1
=2013.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.设⊙O的半径为r,圆心O到直线L的距离为d,若直线L与⊙O有交点,则d与r的关系为( )
| A. | d=r | B. | d<r | C. | d>r | D. | d≤r |
11.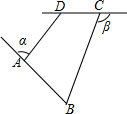 如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
 如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )
如图,已知四边形ABCD,∠α,∠β分别是∠BAD,∠BCD相邻的补角,且∠B+∠ADC=140°,则∠α+∠β等于( )| A. | 140° | B. | 170° | C. | 260° | D. | 120° |
5.设a是最小的质数,b是最大的负整数,c是绝对值最小的实数,则a,b,c三个数的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.
如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.