题目内容
17.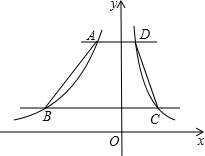 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )| A. | 点A的横坐标是-$\frac{3}{5}$,点B的横坐标是-3 | |
| B. | 点A的横坐标是-$\frac{3}{5}$,点B的纵坐标是$\frac{4}{3}$ | |
| C. | 点A的纵坐标是$\frac{16}{3}$,点B的横坐标是-3 | |
| D. | 点A的纵坐标是$\frac{16}{3}$,点B的纵坐标是$\frac{4}{3}$ |
分析 设两反比例函数的解析式为y1=$\frac{{k}_{1}}{x}$,y2=$\frac{{k}_{2}}{x}$,得出A、B、C、D的坐标,根据AD=1,BC=4,得到$\left\{\begin{array}{l}{{k}_{2}{-}_{1}k=4m}\\{{k}_{2}-{k}_{1}=m+4}\end{array}\right.$,解方程组即可求得m,进而得出A,B的纵坐标.
解答 解:设两反比例函数的解析式为y1=$\frac{{k}_{1}}{x}$,y2=$\frac{{k}_{2}}{x}$,
根据题意得A($\frac{{k}_{1}}{m+4}$,m+4),B($\frac{{k}_{1}}{m}$,m),C($\frac{{k}^{2}}{m}$,m),D($\frac{{k}_{2}}{m+4}$,m+4),
∴$\frac{{k}_{2}}{m+4}$-$\frac{{k}_{1}}{m+4}$=1,$\frac{{k}^{2}}{m}$-$\frac{{k}_{1}}{m}$=4,
整理得$\left\{\begin{array}{l}{{k}_{2}{-}_{1}k=4m}\\{{k}_{2}-{k}_{1}=m+4}\end{array}\right.$,
解得m=$\frac{4}{3}$,
∴A的纵坐标为$\frac{4}{3}$+4=$\frac{16}{3}$,B的纵坐标为$\frac{4}{3}$.
故选D.
点评 本题考查了反比例图象上点的坐标特征,根据题意列出方程组是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
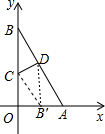 如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).
如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).