题目内容
12.已知-2<x+y<3且1<x-y<4,则z=2x-3y的取值范围是1<z<11.分析 根据不等式的性质,设a(x+y)+b(x-y)=2x-3y;根据不等式的性质来求解;
解答 解:-2<x+y<3 ①,1<x-y<4 ②,
设a(x+y)+b(x-y)=2x-3y
则有$\left\{\begin{array}{l}{a+b=2}\\{a-b=-3}\end{array}\right.$
解得:a=$-\frac{1}{2}$
b=$\frac{5}{2}$
故z=$-\frac{1}{2}(x+y)+\frac{5}{2}(x-y)$,即-$\frac{1}{2}$×(3)+1×$\frac{5}{2}$<z<$-\frac{1}{2}×(-2)+\frac{5}{2}×4$
所以1<z<11
故答案为:1<z<11.
点评 本题考查了了不等式的性质,利用了不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
相关题目
17.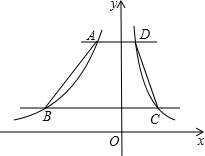 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )| A. | 点A的横坐标是-$\frac{3}{5}$,点B的横坐标是-3 | |
| B. | 点A的横坐标是-$\frac{3}{5}$,点B的纵坐标是$\frac{4}{3}$ | |
| C. | 点A的纵坐标是$\frac{16}{3}$,点B的横坐标是-3 | |
| D. | 点A的纵坐标是$\frac{16}{3}$,点B的纵坐标是$\frac{4}{3}$ |
1.多项式x2+3x-2中,下列说法错误的是( )
| A. | 这是一个二次三项式 | B. | 二次项系数是1 | ||
| C. | 一次项系数是3 | D. | 常数项是2 |
 如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.
如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.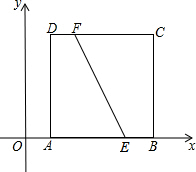 如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0).
如图,在平面直角坐标系中,正方形ABCD的顶点,A、B、C的坐标分别为(1,0)、(5,0)、(5,4),点E、F的坐标分别为(4,0)、(2,4),过EF的中点作直线,若此直线被正方形的两边所截得的线段的长与线段EF的长相等,则这条线段靠近点A的端点的坐标为(1,1)、(1,3)、(2,0). 如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.
如图,将一副三角板的直角顶点重合,可得∠COA=∠DOB,理由是同角的余角相等;若∠AOD=50°,则∠COB=130°.