题目内容
7.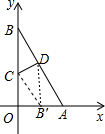 如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).
如图,△AOB中,∠AOB=90°,OA=1,OB=2.折叠纸片,使顶点B落在底边OB上的B′处,折痕为CD,若DB′⊥OA,则点B′的坐标为(2$\sqrt{5}$-4,0).
分析 如图,首先求出AB的长;其次证明BD=B′D(设为λ);由△ADB′∽△ABO,得到$\frac{\sqrt{5}-λ}{\sqrt{5}}=\frac{λ}{2}$=$\frac{AB′}{1}$,求出AB′的长,进而求出OB′的长,即可解决问题.
解答  解:∵∠AOB=90°,OA=1,OB=2,
解:∵∠AOB=90°,OA=1,OB=2,
∴AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$;
由题意得:BD=B′D(设为λ),
则AD=$\sqrt{5}$-λ;而DB′∥BO,
∴△ADB′∽△ABO,
∴$\frac{\sqrt{5}-λ}{\sqrt{5}}=\frac{λ}{2}$=$\frac{AB′}{1}$,
解得:λ=10-4$\sqrt{5}$,AB′=5-2$\sqrt{5}$,
∴OB′=1-AB′=2$\sqrt{5}$-4,
∴点B′的坐标为(2$\sqrt{5}$-4,0).
故答案为(2$\sqrt{5}$-4,0).
点评 该题主要考查了翻折变换的性质、勾股定理、相似三角形的判定及其性质等几何知识点及其应用问题.解题的关键是灵活运用翻折变换的性质等几何知识点来分析、判断、解答.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
12.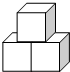 如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
 如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )
如图的几何体是由三个同样大小的立方体搭成的,则下列说法正确的是( )| A. | 主视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
19.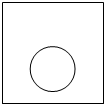 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
 如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )
如图,一个半径为r的圆形纸片在边长为a(a≥2r)的正方形内任意运动,则在该正方形内,这个圆形纸片“不能接触到的部分”的面积为( )| A. | πr2 | B. | a2-πr2 | C. | 4r2-πr2 | D. | $\frac{a^2}{4}$ |
16.已知方程$\frac{x}{2}-\frac{y}{3}=5$,用含x的代数式表示y,下列给出的结论中正确的是( )
| A. | $x=\frac{2y}{3}+10$ | B. | $y=\frac{3x}{2}-15$ | C. | $y=\frac{3x-15}{2}$ | D. | $y=-\frac{3x}{2}+15$ |
17.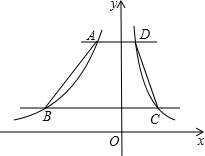 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
 如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )
如图,直角坐标系中,直线y=m+4(m>0)和直线y=m分别与两个反比例函数的图象交于A、D、B、C四点,已知AD=1,BC=4,则关于点A、B两点的坐标说法正确的是( )| A. | 点A的横坐标是-$\frac{3}{5}$,点B的横坐标是-3 | |
| B. | 点A的横坐标是-$\frac{3}{5}$,点B的纵坐标是$\frac{4}{3}$ | |
| C. | 点A的纵坐标是$\frac{16}{3}$,点B的横坐标是-3 | |
| D. | 点A的纵坐标是$\frac{16}{3}$,点B的纵坐标是$\frac{4}{3}$ |
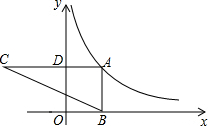 如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4.
如图,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AD⊥y轴于点D,延长AD至点C,使CD=2AD,过点A作AB⊥x轴于点B,连结BC交y轴于点E.若△ABC的面积为6,则k的值为4. 如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.
如图,三角形DEF是由三角形ABC通过平移得到,且点B,E,C,F在同一条直线上,若BF=14,EC=6,则BE的长度是4.