题目内容
11．
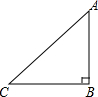如图所示；△ABC是等腰三角形，∠ABC=90°．（1）尺规作图：作线段AB的垂直平分线l，垂足为H．（保留作图痕迹，不写作法）
（2）垂直平分线l交AC于点D，求证：AB=2DH．
分析 （1）利用线段垂直平分线的作法，分别以A，B为端点，大于$\frac{1}{2}$AB为半径作弧，得出直线l即可；
（2）利用利用平行线的性质以及平行线分线段成比例定理得出点D是AC的中点，进而得出答案．
解答 
（1）解：如图所示：直线l即为所求；
（2）证明：∵点H是AB的中点，且DH⊥AB，
∴DH∥BC，
∴点D是AC的中点，
∵DH=$\frac{1}{2}$BC，BC=AB，
∴AB=2DH．
点评 此题主要考查了基本作图以及平行线的性质等知识，熟练掌握平行线分线段成比例定理是解题关键．
练习册系列答案
相关题目
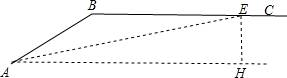某乡间公路有一斜坡AB的坡角为24°36′（即∠BAH=24°36′），斜坡AB的长为100m，路面BC是一段平路，现政府决定把斜坡AB改造成了坡角为12°的斜坡路AE（如图）．
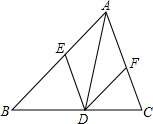如图，已知AD是△ABC的角平分线，点E、F分别是边AC、AB的中点，连接DE、DF，要使四边形AEDF称为菱形，还需添加一个条件，这个条件可以是AB=AC、∠B=∠C或AE=AF（答案不唯一）．．
点P（x，y）在直线x+y=8上，且x＞0，y＞0，点A的坐标为A（6，0），设△OPA的面积为S．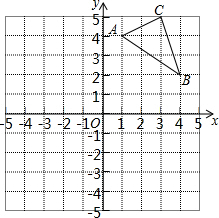
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．
3．
如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：
①BE=$\frac{1}{2}$GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
其中，正确的结论有（ ）
如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=$\frac{1}{2}$GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH
其中，正确的结论有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
