题目内容
6. 点P(x,y)在直线x+y=8上,且x>0,y>0,点A的坐标为A(6,0),设△OPA的面积为S.
点P(x,y)在直线x+y=8上,且x>0,y>0,点A的坐标为A(6,0),设△OPA的面积为S.(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)当S=9时,求点P的坐标.
分析 (1)过点P作PB⊥x轴,垂足为B,则三角形的面积=$\frac{1}{2}•OA•PB$=$\frac{1}{2}×6$×(8-x),从而可得出函数的解析式;
(2)将s=9代入函数的解析式,可求得x的值,然后将x的值代入x+y=8,求得y的值,从而得到点P的坐标.
解答 解:(1)过点P作PB⊥x轴,垂足为B,
由三角形的面积公式可知:S=$\frac{1}{2}•OA•PB$=$\frac{1}{2}×6×(8-x)$即:s=-3x+24.(0<x<8);
(2)将s=9代入s=-3x+24得:x=5,将x=5代入x+y=8得:y=3,
故点P的坐标为(5,3).
点评 本题主要考查的是列函数的关系,能够应用含x的代数式表示PB的长度是解题的关键.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 3m+2n=5mn | B. | (ab2)3=a3b5 | C. | x5•x=x6 | D. | y3÷y3=y |
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.如图,这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据,从中可以看出扣缴电费最多的一次达到( )


| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
16.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-2x-3 | C. | y=2x2+1 | D. | y=5x |
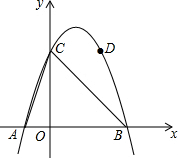 某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.
某拱桥横截面为抛物线形,将抛物线放置在平面直角坐标系中如图所示,抛物线与x轴交于A、B两点,与y轴交于C点,且抛物线的解析式为y=-x2+2x+3.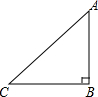 如图所示;△ABC是等腰三角形,∠ABC=90°.
如图所示;△ABC是等腰三角形,∠ABC=90°. 如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.