题目内容
1.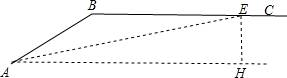 某乡间公路有一斜坡AB的坡角为24°36′(即∠BAH=24°36′),斜坡AB的长为100m,路面BC是一段平路,现政府决定把斜坡AB改造成了坡角为12°的斜坡路AE(如图).
某乡间公路有一斜坡AB的坡角为24°36′(即∠BAH=24°36′),斜坡AB的长为100m,路面BC是一段平路,现政府决定把斜坡AB改造成了坡角为12°的斜坡路AE(如图).(1)求斜坡路AE垂直高度(即EH的长);
(2)坡路AE比坡路AB增加了多少米?(有关三角函数值用计算器计算,或直接用sin24°36′=0.416,cos24°36′=0.9092,tan24°36′=0.4578,sin12°=0.208,cos12°=0.978,tan12°=0.213,最后结果保留整数)
分析 (1)过点B作BD⊥AH于D,则EH=BD.在Rt△ABD中利用AB长和∠BAD的正弦函数值即可求得BD长;
(2)解Rt△AEH,求出AE的长度,再计算AE-AB即可.
解答  解:(1)如图,过点B作BD⊥AH于D,则EH=BD.
解:(1)如图,过点B作BD⊥AH于D,则EH=BD.
在Rt△ABD中,∵∠ADB=90°,∠BAD=24°36′,AB=100m,
∴BD=AB×sin∠BAD=100×0.416=41.6(m),
∴EH=BD≈42m.
即斜坡路AE垂直高度约为42m;
(2)在Rt△AEH中,∵∠AHE=90°,∠EAH=12°,EH=41.6m,
∴AE=$\frac{EH}{sin∠EAH}$=$\frac{41.6}{0.208}$=200(m),
∴AE-AB=200-100=100(m),
即坡路AE比坡路AB增加了100米.
点评 本题考查了解直角三角形的运用,锐角三角函数的运用,坡度坡角的应用.解答时运用三角函数的定义求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列图形中,不是轴对称图形的是( )
| A. |  锐角 | B. |  等腰三角形 | C. |  直角三角形 | D. |  扇形 |
10.下列四个几何体中,主视图与左视图相同的几何体有( )
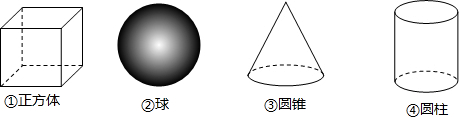

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
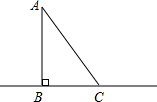 如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)
如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)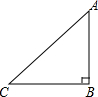 如图所示;△ABC是等腰三角形,∠ABC=90°.
如图所示;△ABC是等腰三角形,∠ABC=90°.