题目内容
在图中,每个小正方形的网格边长都为1,请在下面两幅图中分别画两个形状不同,面积都为20的 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上.
 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上.考点:作图—应用与设计作图
专题:作图题
分析:根据菱形的面积等于对角线乘积的一半,作出一个对角线是10和4的菱形即可;
根据菱形的面积结合网格结构,作底边是5,高是4的菱形即可.
根据菱形的面积结合网格结构,作底边是5,高是4的菱形即可.
解答:解:如图,第一个菱形的对角线分别为10和4,
所以,面积为
×10×4=20,
第二个菱形的底边是5,高为4,
所以,面积是5×4=20.

所以,面积为
| 1 |
| 2 |
第二个菱形的底边是5,高为4,
所以,面积是5×4=20.

点评:本题考查了应用与设计作图,熟练掌握菱形的面积的两种求解方法,结合网格结构以及勾股定理作图是解题的关键.

练习册系列答案
相关题目
要使
、
、(2x-4)0三个式子都有意义,则x的取值范围应为( )
| x+1 |
| 1 | ||
|
A、x>
| ||
| B、x≥-1且x≠2 | ||
C、x>
| ||
D、
|
对于素数p,q,方程x4-px3+q=0有整数解,则p=( )
| A、1 | B、2 | C、3 | D、4 |
一个圆作滚动运动(如图),它从位置A开始,在与它相同的其它六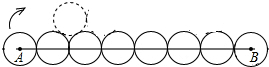 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
 个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.
个圆上部滚动,到达B位置(六个圆的圆心与A、B在同一直线上),则该圆上某一定点绕其圆心共滚过的圈数为( )圈.| A、3 | ||
B、
| ||
C、
| ||
D、
|
若不论k取什么实数,关于x的方程
-
=1(a、b是常数)的根总是x=1,则a+b=( )
| 2kx+a |
| 3 |
| x-bk |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
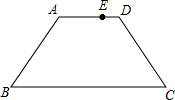 如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象.
如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象.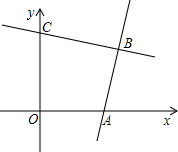 已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.
已知:如图,直线y1=mx-3m与x轴交于点A,直线y2=kx+b与y轴交于点C,两直线交于点B.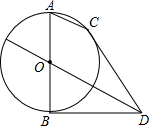 已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD,
已知:如图,AB为⊙O的直径,弦AC∥OD,BD切⊙O于B,连接CD, 如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.