题目内容
 如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.考点:正方形的性质,菱形的性质
专题:几何综合题,压轴题
分析:根据勾股定理求出BE的长度,再根据菱形的四条边都相等,正方形的四条边都相等分别求出CE、CF、DG的长度,然后判定出△DGH和△CFH相似,根据相似三角形对应边成比例列式求出GH与FH的比,最后根据GF=AE=4进行计算即可得解.
解答:解:∵菱形ABCD的边长为5,AE⊥BC于点E,AE=4,
∴BE=
=
=3,
∴CE=BC-BE=5-3=2,
∵正方形AEFG以AE=4为边长,
∴CF=4-2=2,DG=5-4=1,
∵菱形ABCD的边AD∥BC,
∴△DGH∽△CFH,
∴
=
=
,
∴FH=
×4=
.
故答案为:
.
∴BE=
| AB2-AE2 |
| 52-42 |
∴CE=BC-BE=5-3=2,
∵正方形AEFG以AE=4为边长,
∴CF=4-2=2,DG=5-4=1,
∵菱形ABCD的边AD∥BC,
∴△DGH∽△CFH,
∴
| GH |
| FH |
| DG |
| CF |
| 1 |
| 2 |
∴FH=
| 2 |
| 1+2 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查了正方形的性质,菱形的性质,勾股定理的应用,相似三角形的判定与性质,计算出各边的长度,并最后求出GH与FH的比是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
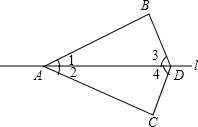 如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )
如图,A、D是直线l上两点,B、C两点位于直线l的两侧,若∠1=∠2,则添加下列哪一个条件后,不能保证△ABD≌△ACD( )| A、AB=AC |
| B、∠3=∠4 |
| C、∠B=∠C |
| D、BD=CD |
 如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D.
如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D. 菱形,要求菱形的顶点均在格点上.
菱形,要求菱形的顶点均在格点上. 如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是
如图,在锐角△ABC中,CD,BE分别是AB,AC上的高,且CD,BE交于点P,若∠A=80°,∠BPC的度数是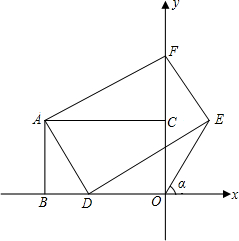 的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF.
的一个动点,连接AD,过A作AD的垂线交y轴于F点,并以AF、AD为边作矩形ADEF. 如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为
如图,正方形OA1B1C1,C1A2B2C2,C2A3B3C3,…的顶点A1,A2,A3,…在直线y=kx+b上,顶点C1,C2,C3,…在x轴上,已知B1(1,1),B2(3,2),那么点A4的坐标为