题目内容
20.已知a2+3a-1=0,则$\frac{{a}^{4}}{{a}^{6}-3{a}^{4}+{a}^{2}}$=$\frac{1}{8}$.分析 原式约分后,将已知等式变形为a2=-3a+1,代入计算即可求出值.
解答 解:∵a2+3a-1=0,即a2=-3a+1,
∴原式=$\frac{{a}^{4}}{{a}^{2}({a}^{4}-3{a}^{2}+1)}$=$\frac{{a}^{2}}{{a}^{4}-3{a}^{2}+1}$=$\frac{-3a+1}{(-3a+1)^{2}+9a-3+1}$=$\frac{-3a+1}{9{a}^{2}+3a-1}$=$\frac{-3a+1}{-27a+9+3a-1}$=$\frac{-3a+1}{-24a+8}$=$\frac{-3a+1}{8(-3a+1)}$=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16. 下列哪个图形经过折叠能围成一个符合条件的正方体( )
下列哪个图形经过折叠能围成一个符合条件的正方体( )
 下列哪个图形经过折叠能围成一个符合条件的正方体( )
下列哪个图形经过折叠能围成一个符合条件的正方体( )| A. |  | B. |  | C. |  | D. |  |
 已知如图,△ACD的外角平分线CB交其外接圆于B,连接BA、BD,求证:BA=BD.
已知如图,△ACD的外角平分线CB交其外接圆于B,连接BA、BD,求证:BA=BD.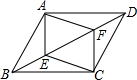 已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形;
已知:如图,在?ABCD中,E、F是对角线BD上的两点,且BE=DF,求证:四边形AECF是平行四边形; 已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF.
已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF.