Question

17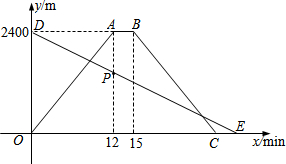．小明从家骑车出发，沿一条直路到相距2400m的书店买书，同时，小明的爸爸以80m/min速度从书店沿同一条路步行回家，小明在书店停留3分钟后沿原路以原速返回．设他们出发x min后，小明与爸爸分别到达离家y₁m、y₂m的地方，图中的折线OABC、线段DE分别表示y₁、y₂与x之间的函数关系．
（1）求点P的坐标，并解释点P的实际意义；
（2）求线段BC所在直线的函数表达式；
（3）小明从书店返回，从开始到追上爸爸需要多长时间？这时他与爸爸离家还有多远？

Answer 1

分析 （1）点P的横坐标代表了爸爸出发的时间，用书店距家的距离减去爸爸出发后走过的距离就能求出点P的纵坐标了；
（2）小明返回的速度没有改变，则所用的时间也为12分钟，从而得出点C坐标为（27，0），将B、C的坐标代入直线BC解析式就可以求出；
（3）小明追上爸爸的时间点即为线段BC与线段DE的交点，利用两条线段解析式可以求出点坐标．

解答 解：（1）∵2400-80×12=2400-960=1440，
∴点P的坐标为（12，1440），
P的实际意义：小明的爸爸从书店出发12分钟后，离家1440米；
（2）∵小明骑车去书店和从书店返回的速度相同，
∴小明从书店返回的时间也为12分钟，
∴C点坐标为（27，0），
设线段BC所在直线的函数表达式为y=kx+b，把点B（15，2400）、点C（27，0）代入得
∴$\left\{\begin{array}{l}15k+b=2400\\ 27k+b=0\end{array}$ 解得$\left\{\begin{array}{l}k=-200\\ b=5400\end{array}$
∴线段BC所在直线的函数表达式为y=-200x+5400（15≤x≤27）；
（3）设线段DE所在直线的函数表达式为y=kx+b，把点D（0，2400）、P（12，1440）代入得
∴$\left\{\begin{array}{l}{b=2400}\\{12k+b=1440}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=-80}\\{b=2400}\end{array}\right.$
∴线段DE所在直线的函数表达式为y-80x+2400（0≤x≤30），
∵小明追上爸爸时两人距家距离相等
∴$\left\{\begin{array}{l}y=-200x+5400\\ y=-80x+2400\end{array}$解得$\left\{\begin{array}{l}x=25\\ y=400\end{array}$
∴25-15=10．
答：小明从书店返回，从开始到追上爸爸需要10分钟．这时他与爸爸离家还有400米．

点评 本题考查了一次函数的应用及一次函数解析式的求法，解题的关键是通过仔细观察图象，从中整理出解题时所需的相关信息．