题目内容
7．春季来临，甲、乙两班学生参加植树造林．甲班每天比乙班少植2棵树，甲班植60棵树所用天数与乙班植70棵树所用天数相同． 求甲班每天植树多少棵．分析 设甲班每天植树x棵，则乙班每天植树（x+2）棵，由“甲班植60棵树所用天数与乙班植70棵树所用天数相等”建立方程求出其解即可．
解答 解：设甲班每天植树x棵．
则根据题意，得$\frac{60}{x}$=$\frac{70}{x+2}$．
解得x=12．
经检验，x=12是原方程的解．且符合题意．
答：甲班每植树12棵．
点评 本题考查了列分式方程解关于工程问题的实际问题的运用，分式方程的解法的运用及工程问题的数量关系的运用，解答时根据甲班植60棵树所用的天数与乙班植70棵树所用的天数相等建立方程是关键．
练习册系列答案
初中学业考试导与练系列答案
相关题目
如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x-3分别与x轴、y轴交于点A、B，点P的坐标为（0，4）．若点M在直线AB上，则PM长的最小值为$\frac{28}{5}$．
19．
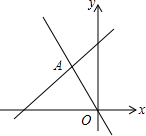如图，在平面直角坐标系中，直线y=-2x和y=ax+4相交于点A（m，3），则不等式-2x＜ax+4的解集为（ ）
如图，在平面直角坐标系中，直线y=-2x和y=ax+4相交于点A（m，3），则不等式-2x＜ax+4的解集为（ ）| A． | x＜-$\frac{3}{2}$ | B． | x＜3 | C． | x＞-$\frac{3}{2}$ | D． | x＞3 |
16．花卉基地种植了郁金香和玫瑰两种花卉共30亩，设种植郁金香x亩，总收益为y万元，有关数据如表：
（1）求y关于x的函数关系式．（收益=销售额-成本）
（2）若计划投入的总成本不超过70万元，要使获得的总收益最大，基地应种植郁金香和玫瑰各多少亩？
（3）已知郁金香每亩地需要化肥400kg，玫瑰每亩地需要化肥600kg．根据（2）中的种植亩数，某地计划运送所需全部化肥，为了提高效率，实际每次运送化肥的总量是原计划的1.25倍，结果运送完全部化肥的次数比原计划少1次，求基地原计划每次运送化肥多少千克？
| 成本 （单位：万元/亩） | 销售额（单位：万元/亩） | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
（2）若计划投入的总成本不超过70万元，要使获得的总收益最大，基地应种植郁金香和玫瑰各多少亩？
（3）已知郁金香每亩地需要化肥400kg，玫瑰每亩地需要化肥600kg．根据（2）中的种植亩数，某地计划运送所需全部化肥，为了提高效率，实际每次运送化肥的总量是原计划的1.25倍，结果运送完全部化肥的次数比原计划少1次，求基地原计划每次运送化肥多少千克？
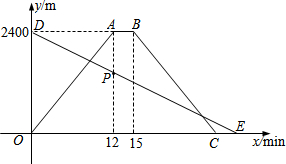小明从家骑车出发，沿一条直路到相距2400m的书店买书，同时，小明的爸爸以80m/min速度从书店沿同一条路步行回家，小明在书店停留3分钟后沿原路以原速返回．设他们出发x min后，小明与爸爸分别到达离家y1m、y2m的地方，图中的折线OABC、线段DE分别表示y1、y2与x之间的函数关系．