题目内容
2. 小明和小刚用如图所示的两个均匀的转盘做配紫色游戏,游戏规则是:分别任意旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.若配成紫色则小刚获胜,否则小明获胜.
小明和小刚用如图所示的两个均匀的转盘做配紫色游戏,游戏规则是:分别任意旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.若配成紫色则小刚获胜,否则小明获胜.(1)请用列表法或树形图求出小明胜的概率;
(2)这个游戏公平吗?请说明理由.
分析 (1)画树状图展示所有9种等可能的结果数,再找出不能配成紫色的结果数,然后根据概率公式求解;
(2)找出能配成紫色的结果数,则根据概率公式计算出小刚胜的概率,然后比较小刚胜的概率和小明胜的概率的大小即可判断这个游戏是否公平.
解答 解:(1)画树状图为:
共有9种等可能的结果数,其中不能配成紫色的结果数为7,
所以小明胜的概率=$\frac{7}{9}$;
(2)这个游戏不公平.理由如下:
因为能配成紫色的结果数为2,
所以小刚胜的概率=$\frac{2}{9}$,
而小明胜的概率=$\frac{7}{9}$;
$\frac{7}{9}$>$\frac{2}{9}$,
所以这个游戏不公平.
点评 本题考查了游戏公平性:判断游戏公平性需要先计算每个事件的概率,然后比较概率的大小,概率相等就公平,否则就不公平.也考查了树状图法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.下列运算结果正确的是( )
| A. | (2x3)2=4x6 | B. | x2+x3=x5 | C. | (-x)-1=$\frac{1}{x}$ | D. | x0=1 |
14.下列计算,正确的是( )
| A. | x3•x4=x12 | B. | (3x)3=27x3 | C. | (x3)3=x6 | D. | 2x2÷x=x |
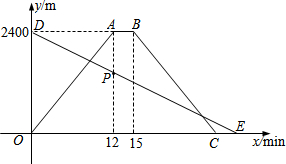 小明从家骑车出发,沿一条直路到相距2400m的书店买书,同时,小明的爸爸以80m/min速度从书店沿同一条路步行回家,小明在书店停留3分钟后沿原路以原速返回.设他们出发x min后,小明与爸爸分别到达离家y1m、y2m的地方,图中的折线OABC、线段DE分别表示y1、y2与x之间的函数关系.
小明从家骑车出发,沿一条直路到相距2400m的书店买书,同时,小明的爸爸以80m/min速度从书店沿同一条路步行回家,小明在书店停留3分钟后沿原路以原速返回.设他们出发x min后,小明与爸爸分别到达离家y1m、y2m的地方,图中的折线OABC、线段DE分别表示y1、y2与x之间的函数关系.