题目内容
8.某商店开学前用2000元购进一批学生书包,开学后发现供不应求,商店又购进第二批同样的书包,所购数量比第一批数量多了20个,但每个书包的进货价比第一批提高了20%,结果购进第二批书包用了3600元.(1)求第一批购进书包时每个书包的进货价是多少元?
(2)若商店想销售第二批书包的利润至少为15%,则每个书包的售价至少定为多少元?(备注:利润率=$\frac{售价-进价}{进价}$×100%)
分析 (1)设第一批购进书包时每个书包的进货价是x元,则第二批的进货价为(1+20%)x元,根据题意,第二批所购数量比第一批数量多了20个,列方程求解;
(2)设每个书包至少定价为y元,根据题意得出不等式解答即可.
解答 解:(1)设第一批购进书包的进货价是x元,则第二批书包的进价是1.2x元,
$\frac{2000}{x}+20=\frac{3600}{1.2x}$,
解得:x=50,
经检验:x=50是原方程的解,
答:第一批购进书包的进货价是50元;
(2)设每个书包至少定价为y元,得:
$\frac{y-50(1+20%)}{50×(1+20%)}×100%≥15%$,
解得:y≥69,
答:设每个书包至少定价为69元.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,射出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
相关题目
19.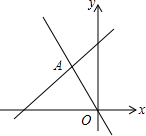 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
 如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )
如图,在平面直角坐标系中,直线y=-2x和y=ax+4相交于点A(m,3),则不等式-2x<ax+4的解集为( )| A. | x<-$\frac{3}{2}$ | B. | x<3 | C. | x>-$\frac{3}{2}$ | D. | x>3 |
16.花卉基地种植了郁金香和玫瑰两种花卉共30亩,设种植郁金香x亩,总收益为y万元,有关数据如表:
(1)求y关于x的函数关系式.(收益=销售额-成本)
(2)若计划投入的总成本不超过70万元,要使获得的总收益最大,基地应种植郁金香和玫瑰各多少亩?
(3)已知郁金香每亩地需要化肥400kg,玫瑰每亩地需要化肥600kg.根据(2)中的种植亩数,某地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的1.25倍,结果运送完全部化肥的次数比原计划少1次,求基地原计划每次运送化肥多少千克?
| 成本 (单位:万元/亩) | 销售额(单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
(2)若计划投入的总成本不超过70万元,要使获得的总收益最大,基地应种植郁金香和玫瑰各多少亩?
(3)已知郁金香每亩地需要化肥400kg,玫瑰每亩地需要化肥600kg.根据(2)中的种植亩数,某地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的1.25倍,结果运送完全部化肥的次数比原计划少1次,求基地原计划每次运送化肥多少千克?
3.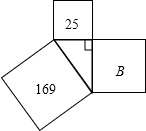 如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
 如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )| A. | 144 | B. | 194 | C. | 12 | D. | 169 |
18.某小区共有5000个家庭,为了了解辖区居民的住房情况,居民委员会随机调查了本辖区内一定数量的家庭的住房面积,并将调查的资料绘制成直方图和扇形图.(m~n中含右端点,不含左端点)
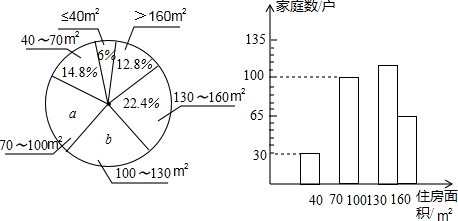
请你根据以上不完整的直方图和扇形图提供的信息,解答下列问题:
(1)这次共调查了多少个家庭的住房面积?扇形图中的a、b的值分别是多少?
(2)补全频数分布直方图;
(3)被调查的家庭中,在未来5年内,计划购买第二套住房的家庭统计如下表:
根据这次调查,估计本小区在未来的5年内,共有多少个家庭计划购买第二套住房?

请你根据以上不完整的直方图和扇形图提供的信息,解答下列问题:
(1)这次共调查了多少个家庭的住房面积?扇形图中的a、b的值分别是多少?
(2)补全频数分布直方图;
(3)被调查的家庭中,在未来5年内,计划购买第二套住房的家庭统计如下表:
| 住房面和(m2) | ≤40 | 40~70 | 70~100 | 100~130 | 130~160 | >160 |
| $\frac{计划购第二套房的家庭数}{被调查的家庭数}$ | 0 | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{32}$ |
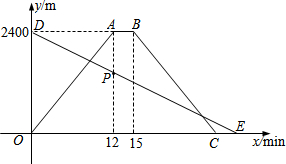 小明从家骑车出发,沿一条直路到相距2400m的书店买书,同时,小明的爸爸以80m/min速度从书店沿同一条路步行回家,小明在书店停留3分钟后沿原路以原速返回.设他们出发x min后,小明与爸爸分别到达离家y1m、y2m的地方,图中的折线OABC、线段DE分别表示y1、y2与x之间的函数关系.
小明从家骑车出发,沿一条直路到相距2400m的书店买书,同时,小明的爸爸以80m/min速度从书店沿同一条路步行回家,小明在书店停留3分钟后沿原路以原速返回.设他们出发x min后,小明与爸爸分别到达离家y1m、y2m的地方,图中的折线OABC、线段DE分别表示y1、y2与x之间的函数关系.