题目内容
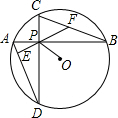 如图,⊙O的半径为4
如图,⊙O的半径为4| 5 |
(1)求证:EF⊥AD;
(2)若AB=16,OP=2
| 13 |
考点:垂径定理,勾股定理,圆周角定理
专题:证明题
分析:(1)由AB⊥CD得∠BPC=∠APD=90°,根据斜边上中线性质得PF=FB,则∠B=∠FPB,根据对顶角相等得∠FPB=∠APE,根据圆周角定理得∠B=∠D,所以∠APE=∠D,而∠APE+∠DPE=90°,所以∠D+∠DPE=90°,于是得到EF⊥AD;
(2)过O点作OM⊥AB于M,ON⊥CD于N,连结OB、OD,根据垂径定理得BM=
AB=8,DN=
CD,在Rt△BOM中,根据勾股定理计算出OM=4,在Rt△OPM中,计算出PM=6,则ON=PM=6,在Rt△OND中,根据勾股定理计算出DN=2
,所以CD=2DN=4
.
(2)过O点作OM⊥AB于M,ON⊥CD于N,连结OB、OD,根据垂径定理得BM=
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 11 |
解答: (1)证明:∵AB⊥CD,
(1)证明:∵AB⊥CD,
∴∠BPC=∠APD=90°,
∵F点为BC的中点,
∴PF=FB,
∴∠B=∠FPB,
而∠FPB=∠APE,∠B=∠D,
∴∠APE=∠D,
而∠APE+∠DPE=90°,
∴∠D+∠DPE=90°,
∴∠PED=90°,
∴EF⊥AD;
(2)解:过O点作OM⊥AB于M,ON⊥CD于N,连结OB、OD,如图,
∴BM=
AB=
×16=8,DN=
CD,
在Rt△BOM中,OB=4
,
∴OM=
=4,
在Rt△OPM中,OP=2
,
∴PM=
=6,
∴ON=PM=6,
在Rt△OND中,OD=4
,
∴DN=
=2
,
∴CD=2DN=4
.
 (1)证明:∵AB⊥CD,
(1)证明:∵AB⊥CD,∴∠BPC=∠APD=90°,
∵F点为BC的中点,
∴PF=FB,
∴∠B=∠FPB,
而∠FPB=∠APE,∠B=∠D,
∴∠APE=∠D,
而∠APE+∠DPE=90°,
∴∠D+∠DPE=90°,
∴∠PED=90°,
∴EF⊥AD;
(2)解:过O点作OM⊥AB于M,ON⊥CD于N,连结OB、OD,如图,
∴BM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BOM中,OB=4
| 5 |
∴OM=
| OB2-BM2 |
在Rt△OPM中,OP=2
| 13 |
∴PM=
| OP2-OM2 |
∴ON=PM=6,
在Rt△OND中,OD=4
| 5 |
∴DN=
| OD2-ON2 |
| 11 |
∴CD=2DN=4
| 11 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和勾股定理.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
在根式
,
,
,
,
中最简二次根式的个数是 ( )
| 3 |
| x2+6x+9 |
| a2+b2 |
| (x+y)(x2-y2) |
|
| A、2个 | B、3个 | C、4个 | D、5个 |
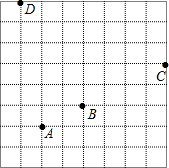 如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
如图,是一个规格为8×8的球桌,小明用A球撞击B球,到C处反弹,再撞击桌边D处,请选择适当的平面直角坐标系,并用坐标表示各点的位置.
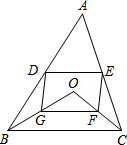 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E. 如图,抛物线y=x2沿直线y=x向上平移
如图,抛物线y=x2沿直线y=x向上平移 如图,甲、乙两个长方形有一部分重叠在一起,甲长方形不重叠的部分是甲长方形面积的
如图,甲、乙两个长方形有一部分重叠在一起,甲长方形不重叠的部分是甲长方形面积的 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.