题目内容
 如图,甲、乙两个长方形有一部分重叠在一起,甲长方形不重叠的部分是甲长方形面积的
如图,甲、乙两个长方形有一部分重叠在一起,甲长方形不重叠的部分是甲长方形面积的| 3 |
| 4 |
| 5 |
| 6 |
考点:一元一次方程的应用
专题:几何图形问题
分析:设甲长方形的面积为xcm2,乙长方形的面积为(100-x)cm2,根据甲、乙两个长方形重合面积相等建立方程求出其解即可.
解答:解:设甲长方形的面积为xcm2,乙长方形的面积为(100-x)cm2,由题意,得
(1-
)x=(1-
)(100-x),
解得:x=40.
∴重叠部分面积是:40×(1-
)=10cm2.
故答案为:10
(1-
| 3 |
| 4 |
| 5 |
| 6 |
解得:x=40.
∴重叠部分面积是:40×(1-
| 3 |
| 4 |
故答案为:10
点评:本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,解答时根据甲、乙两个长方形重合面积相等建立方程是关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
用科学记数法表示0.0000907的结果正确的是( )
| A、9.1×10-4 |
| B、9.1×10-5 |
| C、9.0×10-5 |
| D、9.07×10-5 |
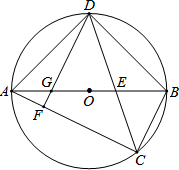 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.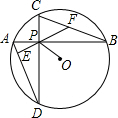 如图,⊙O的半径为4
如图,⊙O的半径为4 如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=140°,则∠AOE的大小为