题目内容
 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.①abc>0;②2a+b=0;③方程ax2+bx+c=0(a≠0)必有两个不相等的实根;④a+b+c>0;⑤当函数值y随x的逐渐增大而减小时,必有x≤1.
| A、1 | B、2 | C、3 | D、4 |
考点:二次函数图象与系数的关系
专题:
分析:根据二次函数图象开口向下确定出a是负数,由抛物线与y轴交于正半轴判断c是正数,根据对称轴在y轴的右边确定出b是正数,再根据有理数乘法符号法则即可判断①;
根据对称轴为直线x=1即可判断②;
根据抛物线与x轴的交点个数即可判断③;
根据x=1时的函数值判断a+b+c是正数,即可判断④;
根据二次函数的增减性判断x≤1时的增减情况,即可判断⑤.
根据对称轴为直线x=1即可判断②;
根据抛物线与x轴的交点个数即可判断③;
根据x=1时的函数值判断a+b+c是正数,即可判断④;
根据二次函数的增减性判断x≤1时的增减情况,即可判断⑤.
解答:解:①∵图象开口向下,与y轴交于正半轴,对称轴在y轴右侧,
∴a<0,c>0,-
>0,b>0,
∴abc<0,故本小题错误;
②∵对称轴直线x=-
=1,
∴2a=-b,
∴2a+b=0,故本小题正确;
③∵二次函数与x轴有两个交点,
∴方程ax2+bx+c=0(a≠0)必有两个不相等的实根,故本小题正确;
④当x=1时,函数值为正数,所以,a+b+c>0,故本小题正确;
⑤当x≤1时,函数值y随x的逐渐增大而增大,故本小题错误;
综上所述,不正确的有①⑤共两个.
故选B.
∴a<0,c>0,-
| b |
| 2a |
∴abc<0,故本小题错误;
②∵对称轴直线x=-
| b |
| 2a |
∴2a=-b,
∴2a+b=0,故本小题正确;
③∵二次函数与x轴有两个交点,
∴方程ax2+bx+c=0(a≠0)必有两个不相等的实根,故本小题正确;
④当x=1时,函数值为正数,所以,a+b+c>0,故本小题正确;
⑤当x≤1时,函数值y随x的逐渐增大而增大,故本小题错误;
综上所述,不正确的有①⑤共两个.
故选B.
点评:本题考查了二次函数图象与系数的关系,主要涉及二次函数图象的开口方向,对称轴,与x轴的交点,取特殊值判断系数的和的情况,二次函数的增减性.

练习册系列答案
相关题目
抛物线y=ax2+bx+c的图象向左平移2个单位,再向上平移1个单位后得抛物线y=-2x2,则原抛物线的解析式为( )
| A、y=-2(x+2)2-1 |
| B、y=-2(x+2)2+1 |
| C、y=-2(x+1)2+2 |
| D、y=-2(x-2)2-1 |
3个连续偶数的和为36,则它们的积为( )
| A、1868 | B、1680 |
| C、1200 | D、998 |
用科学记数法表示0.0000907的结果正确的是( )
| A、9.1×10-4 |
| B、9.1×10-5 |
| C、9.0×10-5 |
| D、9.07×10-5 |
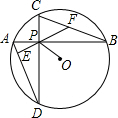 如图,⊙O的半径为4
如图,⊙O的半径为4 如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( )
如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( )