题目内容
已知,在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B.
(1)如图1,求证:CD⊥AB;
(2)请写出你在(1)的证明过程中应用的两个互逆的真命题;
(3)将△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
①如图2,若∠B=34°,求∠A′CB的度数;
②若∠B=n°,请直接写出∠A′CB的度数(用含n的代数式表示).

(1)如图1,求证:CD⊥AB;
(2)请写出你在(1)的证明过程中应用的两个互逆的真命题;
(3)将△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
①如图2,若∠B=34°,求∠A′CB的度数;
②若∠B=n°,请直接写出∠A′CB的度数(用含n的代数式表示).

考点:翻折变换(折叠问题)
专题:计算题
分析:(1)根据直角三角形中两锐角互余得∠A+∠B=90°,而∠ACD=∠B,则∠A+∠ACD=90°,所以∠ADC=90°,然后根据垂直的定义得CD⊥AB;
(2)有(1)得到两个互逆的真命题为:直角三角形中两锐角互余;两锐角互余的三角形为直角三角形;
(3)①先得到∠ACD=34°,∠BCD=56°,再根据折叠的性质得∠A′CD=∠ACD=34°,然后利用∠A′CB=∠BCD-∠A′CD求解;
②与①的计算方法一样.
(2)有(1)得到两个互逆的真命题为:直角三角形中两锐角互余;两锐角互余的三角形为直角三角形;
(3)①先得到∠ACD=34°,∠BCD=56°,再根据折叠的性质得∠A′CD=∠ACD=34°,然后利用∠A′CB=∠BCD-∠A′CD求解;
②与①的计算方法一样.
解答:解:(1)∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB;
(2)两个互逆的真命题为:直角三角形中两锐角互余;两锐角互余的三角形为直角三角形;
(3)①∵∠B=34°,
∴∠ACD=34°,
∴∠BCD=90°-34°=56°,
∵△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
∴∠A′CD=∠ACD=34°,
∴∠A′CB=∠BCD-∠A′CD=56°-34°=22°;
②∵∠B=n°,
∴∠ACD=n°,
∴∠BCD=90°-n°,
∵△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
∴∠A′CD=∠ACD=n°,
∴∠A′CB=∠BCD-∠A′CD=90°-n°-n°=90°-2n°.
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB;
(2)两个互逆的真命题为:直角三角形中两锐角互余;两锐角互余的三角形为直角三角形;
(3)①∵∠B=34°,
∴∠ACD=34°,
∴∠BCD=90°-34°=56°,
∵△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
∴∠A′CD=∠ACD=34°,
∴∠A′CB=∠BCD-∠A′CD=56°-34°=22°;
②∵∠B=n°,
∴∠ACD=n°,
∴∠BCD=90°-n°,
∵△ADC沿CD所在直线翻折,A点落在BD边所在直线上,记为A′点,
∴∠A′CD=∠ACD=n°,
∴∠A′CB=∠BCD-∠A′CD=90°-n°-n°=90°-2n°.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
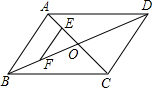 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )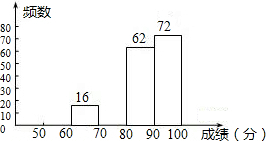 某区八年级有3000名学生参加“心理健康知识竞赛”活动.
某区八年级有3000名学生参加“心理健康知识竞赛”活动.

 如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.
如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.