题目内容
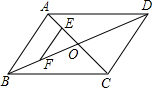如图，?ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC+BD=24cm，△OAB的周长是18cm，则EF的长为（ ）| A、6 | B、4 | C、3 | D、2 |
考点：三角形中位线定理,平行四边形的性质
专题：
分析：根据AC+BD=24厘米，可得出出OA+OB=12cm，继而求出AB，判断EF是△OAB的中位线即可得出EF的长度．
解答：解：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
又∵AC+BD=24厘米，
∴OA+OB=12cm，
∵△OAB的周长是18厘米，
∴AB=6cm，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=
AB=3cm．
故选C．
∴OA=OC，OB=OD，
又∵AC+BD=24厘米，
∴OA+OB=12cm，
∵△OAB的周长是18厘米，
∴AB=6cm，
∵点E，F分别是线段AO，BO的中点，
∴EF是△OAB的中位线，
∴EF=
| 1 |
| 2 |
故选C．
点评：本题考查了三角形的中位线定理，解答本题需要用到：平行四边形的对角线互相平分，三角形中位线的判定定理及性质．
练习册系列答案
阅读快车系列答案
相关题目
如图，若AB∥CD∥EF，∠B=40°，∠F=30°，则∠BCF=当x=-2时，下列不等式成立的是（ ）
| A、x-5＞-7 | ||
B、
| ||
| C、2（x-2）＞-2 | ||
| D、3x＞2x |
| 9 |
| A、-3 | ||
| B、3 | ||
| C、±3 | ||
D、
|
我县现有人口13万5千人，用科学记数法表示为（ ）
| A、1.35×104 |
| B、1.35×104 |
| C、0.135×106 |
| D、1.35×105 |
如果ab＞0 bc＜0 那么y=-
x-
不经过（ ）象限．
| a |
| b |
| c |
| b |
| A、一 | B、二 | C、三 | D、四 |
若一元二次方程2x2+2x+m=0有一个实数解x=1，则m的取值是（ ）
| A、m=-4 | ||
| B、m=1 | ||
| C、m=4 | ||
D、m=
|
