题目内容
二次函数y= ax2+bx+c(a≠0)的图象如图2-130所示,根据图象解
ax2+bx+c(a≠0)的图象如图2-130所示,根据图象解
答下列问题.
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4 )若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.

解:(1)由二次函数y=ax2+bx+c(a≠0)的图象可知,抛物线与x轴交于(1,0),B(3,0)两点,即x=1或x=3是方程ax2+bx+c=0的两个根.
(2)不等式ax2+bx+c>0的解集, 即是求y>0的解集,由图象可知l<x<3.
即是求y>0的解集,由图象可知l<x<3.
(3)因为a<0,故在对称轴的右侧y随x的增大而减小,即当x>2时,y随x的增大而减小.
(4)由图可知, 解得
解得 代入方程得-2x2+8x-6-k=O.又因为方程有两个不相等的实数根,所以△>0,即82-4×(-2)×(-6-k)>0,解得k<2.
代入方程得-2x2+8x-6-k=O.又因为方程有两个不相等的实数根,所以△>0,即82-4×(-2)×(-6-k)>0,解得k<2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是____________.
二次函数y=x2+bx+c的图象经过点(-1,0),(1,-2),当y随x的增大而增大时,x的取值范围是____________.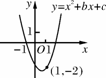
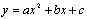 的图象如图 l-2-32所示,则下列结论错误的是( )
的图象如图 l-2-32所示,则下列结论错误的是( ) 的两根之和为负
的两根之和为负
 y=-x2+4x-3,其图象与y轴交于点B
y=-x2+4x-3,其图象与y轴交于点B ,与x轴交于A, C 两点. 求△ABC的周长和面积.
,与x轴交于A, C 两点. 求△ABC的周长和面积. 外 B.在⊙P上 C.在⊙
外 B.在⊙P上 C.在⊙ P内 D.不能确定
P内 D.不能确定 中,
中, 为
为 的直径,
的直径, ,则
,则 的度数是 度.
的度数是 度. .
.
 B. πR2 C.
B. πR2 C. D.
D.