题目内容
7.在△ABC中,AB=AC=3,BC=2,求:(1)△ABC的面积S△ABC及AC边上的高BE;
(2)△ABC的内切圆的半径r;
(3)△ABC的外接圆的半径R.
分析 (1)根据题意可知△ABC为等腰三角形,根据三角形面积计算公式S=底×高÷2计算三角形面积公式;
(2)利用等面积,求△ABC的△内切圆的半径r;
(3)利用勾股定理,求△ABCr外接圆的半径R.
解答 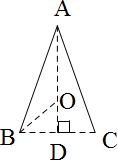 解:(1)过点A作AD⊥BC于点D,则AD为BC边上的高,
解:(1)过点A作AD⊥BC于点D,则AD为BC边上的高,
∵AB=AC=3,
∴点D为BC的中点,DB=$\frac{1}{2}BC$=1,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
∴${S}_{△ABC}=\frac{1}{2}BC×AD=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$,
由${S}_{△ABC}=\frac{1}{2}BE•AC=2\sqrt{2}$,可得BE=$\frac{4\sqrt{2}}{3}$.
(2)由等面积可得,
${S}_{△ABC}=2\sqrt{2}=\frac{1}{2}(3+3+2)r$,
∴r=$\frac{\sqrt{2}}{2}$,
(3)由勾股定理可得,
${R}^{2}=(2\sqrt{2}-R)^{2}+{1}^{2}$,
∴$R=\frac{9\sqrt{2}}{8}$
点评 本试题考查三角形的面积公式和转化的思想,正确理解三角形的内切圆和外接圆,正确应用勾股定理是求解的关键.

练习册系列答案
相关题目
7.下列方程中,有实数解的是( )
| A. | x2+1=0 | B. | x3+1=0 | C. | $\sqrt{x+1}=-2$ | D. | $\frac{x}{x-2}=\frac{2}{x-2}$ |
8.下列方程是一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=3 | B. | x2+x=y | C. | (x-4)(x+2)=3 | D. | 3x-2y=0 |
5.若一个二元一次方程的一个解为$\left\{{\begin{array}{l}{x=2}\\{y=-1}\end{array}}\right.$,则这个方程可以是( )
| A. | x+y=1 | B. | x-y=1 | C. | y-x=1 | D. | x+2y=1 |
 如图,直线与y轴的交点是(0,-3),当x<0时,y的取值范围是y>-3.
如图,直线与y轴的交点是(0,-3),当x<0时,y的取值范围是y>-3.