题目内容
17．
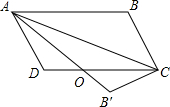如图，在平行四边形ABCD中将△ABC沿AC对折，使点B落在B′处，AB′和CD相交于O，求证：OD=OB′．
分析 利用翻折不变性以及平行四边形的性质先证明AB′=CD，再证明OA=OC即可．
解答 证明：∵△ACB′是由△ABC翻折，
∴∠BAC=∠CAB′，AB=AB′，
∵四边形ABCD是平行四边形，
∴AB∥BC，AB=DC，
∴∠BAC=∠ACO，
∴∠OAC=∠OCA，
∴OA=OC，
∵AB′=CD，
∴OD=OB′．
点评 本题考查平行四边形的性质、翻折变换、等腰三角形的判定和性质等知识，解题的关键是利用翻折不变性发现等腰三角形，属于中考常考题型．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
7．（-2xy）4的计算结果是（ ）
| A． | -2x4y4 | B． | 8x4y4 | C． | 16xy4 | D． | 16x4y4 |
8．在“等边三角形、正方形、等腰梯形、平行四边形、矩形、正六边形”中，任取其中一个圆形，恰好是中心对称图形的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
2．一质地均匀的正四面体，其四个面上分别画出圆、等边三角形、菱形、正五边形，投掷该四面体一次，则向下一面的图形是轴对称图形但不是中心对称图形的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | 1 |
6．$\frac{1}{6}$的绝对值是（ ）
| A． | -6 | B． | 6 | C． | -$\frac{1}{6}$ | D． | $\frac{1}{6}$ |
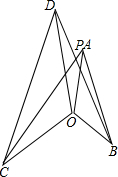如图，△AOB与△COD中，OA=OB，OC=OD，∠AOB=∠COD，AC与BD交于点P．