Question

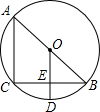如图，AB是⊙O的直径，BC是弦，OD⊥BC，垂足为E，交⊙O于D，连接AC．
（1）请写出3个不同类型的正确结论；
（2）若BC=8，ED=2，求⊙O的半径．

Answer 1

考点：垂径定理,圆周角定理

专题：

分析：（1）根据垂径定理及平行线的性质可得出结论；
（2）设⊙O的半径为r，先根据垂径定理求出BE的长，再根据勾股定理即可得出r的长．

解答：解：（1）∵AB是⊙O的直径，
∴∠ACB=90°；
∵OD⊥BC，
∴CF=BE；
∵∠ACB=90°，OD⊥BC，
∴AC∥OD；

（2）设⊙O的半径为r，
∵OD⊥BC，BC=8，
∴BE=

1

2

BC=4，
∵ED=2，
∴OB²=BE²+OE²，即r²=4²+（r-2）²，解得r=5．

点评：本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．