题目内容
3. 如图,在四边形ABCD中,AC平分∠BAD,且BC=CD,求证:∠B+∠D=180°.
如图,在四边形ABCD中,AC平分∠BAD,且BC=CD,求证:∠B+∠D=180°.
分析 过C作CE⊥AB于点E,作CF⊥AD交AD的延长线与点F,则可证得Rt△BCE≌Rt△DCF,利用全等三角形的性质可证得结论.
解答 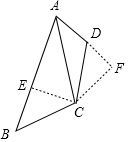 证明:
证明:
如图,过C作CE⊥AB于点E,作CF⊥AD交AD的延长线与点F,
∵AC平分∠BAD,
∴CE=CF,
在Rt△BCE和Rt△DCF中
$\left\{\begin{array}{l}{BC=CD}\\{CE=CF}\end{array}\right.$
∴Rt△BCE≌Rt△DCF(HL),
∴∠B=∠CDF,
∵∠CDF+∠ADC=180°,
∴∠B+∠ADC=180°.
点评 本题主要考查全等三角形的判定和性质,由角平分线的性质构造三角形全等是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
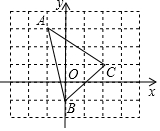 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,3),B(0,-1),C(2,1). 如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数.
如图,直线a、b交于O点,夹角为45°,A、B分别为直线a,b上异于O的点,P为同一平面内不在直线a,b上的定点,且P、A、B不共线,求当△PAB的周长为最小值时,∠APB的度数. 一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是x<3.
一次函数y=kx+b的图象如图所示,则不等式kx+b>0的解集是x<3.