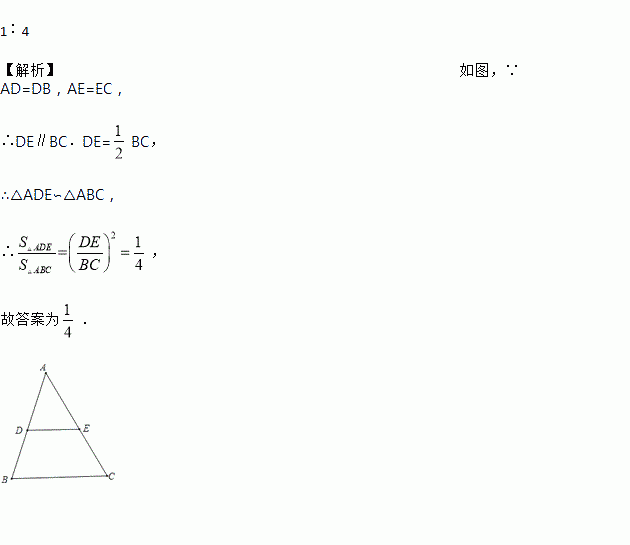题目内容
在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是______.
1∶4
【解析】如图，∵AD=DB，AE=EC，
∴DE∥BC．DE=BC，
∴△ADE∽△ABC，
∴，
故答案为．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，已知E，F是AC上的两点，AE=CF，DF=BE，∠AFD=∠CEB，则下列不成立的是（ ）
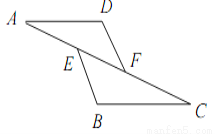
A. ∠A=∠C B. AD=CB C. BC=DF D. DF∥BE
C
【解析】∵AE＝CF（已知），
∴AE+EF＝EF+CF，
∴AF＝EC，
∵∠AFD=∠CEB，
∴△AFD≌△CEB（SAS），
∴∠A=∠C，
AD=CB，BC=DA，
∵∠AFD=∠CEB，
∴DF∥BE.
故选：C. 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（ ）
A．7 B．7或8 C．8或9 D．7或8或9
D．
【解析】
试题分析：设内角和为1080°的多边形的边数是n，则（n﹣2）•180°=1080°，解得：n=8．
则原多边形的边数为7或8或9．故选D． 如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，A′、B′、C′分别为EF、EG、GF的中点，△A′B′C′的周长为_________．如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n个三角形的周长是__________________．
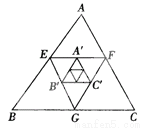
16
【解析】∵如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，
∴EF、FG、EG为三角形中位线，
∴EF=BC，EG=AC，FG=AB，
∴EF+FG+EG=（BC+AC+AB），即△EFG的周长是△ABC周长的一半，
同理，△A′B′C′的周长是△EFG的周长的一半，即△A′B′C′的周长为×64=16，
以此类推，第n个小三角形的周长... 如图，已知△ABC中，D为AB的中点．
（1）请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，若DE=4，求BC的长．
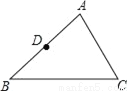
（1）作图见解析;（2）BC=8．
【解析】试题分析：（1）作线段的垂直平分线即可．
（2）根据三角形中位线定理即可解决．
试题解析：（1）作线段的垂直平分线交于,点就是所求的点．
（2）分别为的中点， 工人小王4月份计划生产零件270个，前 10天平均每天生产5个，后来改进技术，提前3天超额完成任务．设小王10天之后平均每天生产零件x个，请你试着写出x所满足的关系式．
50＋（20－3）x＞270
【解析】试题分析：首先设小王10天之后平均每天生产零件x个，利用4月份计划生产零件270个，改进技术后提前3天超额完成任务，进而得出不等式即可．
试题解析：设小王10天之后平均每天生产零件x个，根据题意得
50+（20-3）x＞270． 从2，3，4，5，6中任取两个数就组成一组数，其中两数之和小于10的数组共有 组．
8
【解析】
试题分析：将所有情况列举出来，然后判断即可．
【解析】
从2，3，4，5，6中任取两个数就组成一组数，可能为2+3=5，2+4=6，2+5=7，2+6=8，3+4=7，3+5=8，3+6=9，4+5=9，4+6=10，5+6=11，
其中小于10的有8组，
故答案为：8． 如图，△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的，若∠1: ∠2:∠3 = 28 :5 : 3， 则∠4的度数为__________
80°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
【解析】
∵∠1: ∠2:∠3 = 28 :5 : 3，
∠1+∠2+∠3 = 180°，
∴∠1=140°，∠2=25°，∠3=15°，
由翻折得∠EBA =∠2 =25°，∠DCA =∠3 =15°，
∴∠EBC=∠EBA +∠2 =50°，∠DC... 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C.