题目内容
5.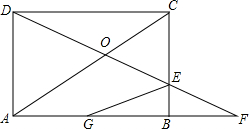 如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).
如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).(1)t为何值时,GE∥AC?
(2)t为何值时,E在GF的中垂线上?
分析 (1)利用相似三角形△BGE∽△BAC的对应边成比例进行解答;
(2)当E在GF的中垂线上时,BG=BF,据此来求t的值.
解答  解:(1)当GE∥AC时,△BGE∽△BAC,则$\frac{BG}{AB}$=$\frac{BE}{BC}$,即$\frac{8-2t}{8}$=$\frac{t}{6}$,
解:(1)当GE∥AC时,△BGE∽△BAC,则$\frac{BG}{AB}$=$\frac{BE}{BC}$,即$\frac{8-2t}{8}$=$\frac{t}{6}$,
解得 t=$\frac{12}{5}$.
即当t=$\frac{12}{5}$时,GE∥AC;
(2)如图,∵四边形ABCD是矩形,点F在AB的延长线上,
∴CD∥AF,
∴△CDE∽△BFE,
∴$\frac{CD}{BF}$=$\frac{CE}{BE}$,即$\frac{8}{BF}$=$\frac{6-t}{t}$,则BF=$\frac{8t}{6-t}$,①
又∵E在GF的中垂线上,
∴BG=BF,即8-2t=BF,②
由①②得到:8-2t=$\frac{8t}{6-t}$,
解得t1=2,t2=12,
∵0<t<4,
∴t2=12,舍去.
即t=2时,E在GF的中垂线上.
点评 本题考查了四边形综合题.解题过程中,涉及到了矩形的性质、相似三角形的判定与性质的综合运用.解答(2)题时,同时要注意t的取值范围,从而对t不同值的取舍作出正确的判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在3.14,0.1010010…,π,$\sqrt{9}$,$\frac{\sqrt{2}}{2}$,-$\frac{22}{7}$,-$\root{3}{4}$这些实数中无理数有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13. 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
 如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )
如图,已知AB⊥BD,AC⊥CD,∠A=40°,则∠D的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$.
如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$. 如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.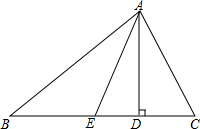 如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论:
如图,过△ABC的顶点A分别作对边BC上的高AD和中线AE,D为垂足,E为BC的中点,规定λA=$\frac{DE}{BE}$,特别地,当点D与E重合时,规定λA=0.对λB、λC作类似的规定.给出下列结论: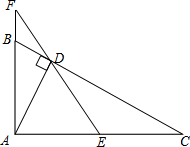 如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证:
如图,已知∠BAC=90°,AD⊥BC于D,E是AC的中点,ED的延长线交AB的延长线于点F.求证: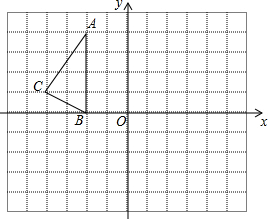 如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题:
如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(-2,4)、(-2,0)、(-4,1),结合所给的平面直角坐标系解答下列问题: 如图,△BEC和△ADC都是等腰直角三角形,∠BEC=∠ADC=90°,A,E,C在一条直线上,求证:AB=$\sqrt{2}$DE.
如图,△BEC和△ADC都是等腰直角三角形,∠BEC=∠ADC=90°,A,E,C在一条直线上,求证:AB=$\sqrt{2}$DE.