题目内容
15. 如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$.
如图,线段AB、CD相交于点E,AD∥EF∥BC.若AE:EB=1:2,S△ADE=1,则AF:AC=$\frac{1}{3}$,S△AEF=$\frac{2}{3}$.
分析 已知AD∥EF∥BC,根据平行线分线段成比例定理,可得出AE:EB=AF:FC,也就求出AF与AC的比例关系;由于△ADE和△AEF等高,因此它们的面积比等于底边比,已知了EF、AD的比例关系,根据△ADE的面积即可求出△AEF的面积.
解答 解:∵AD∥EF∥BC,
∴$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$,
∴AF:AC=$\frac{1}{3}$,$\frac{EF}{AD}$=$\frac{CF}{AD}$=$\frac{2}{3}$,
∴S△AEF:S△ADE=EF:AD=2:3,
∵S△ADE=1,
∴S△AEF=$\frac{2}{3}$.
故答案为:$\frac{1}{3}$,$\frac{2}{3}$.
点评 该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入把握题意,灵活运用相似三角形的判定及其性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3. 如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )
如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )
 如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )
如图,Rt△ABC∽Rt△ADE,∠BCA=30°,F,M,N分别为BE,BC,DE的中点.①△BDA∽△CEA;②BD⊥CE;③∠MFN=90°;④MF=2NF.上述结论中正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.下列说法中正确的是( )
| A. | 同位角相等 | B. | 邻补角相等 | ||
| C. | 垂线段最短 | D. | 平行同一条直线的两条直线平行 |
 在平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1)找一点D,使四边形ABCD是平行四边形,求点D的坐标.
在平面直角坐标系中,点A、B、C的坐标分别是A(-2,5),B(-3,-1),C(1,-1)找一点D,使四边形ABCD是平行四边形,求点D的坐标.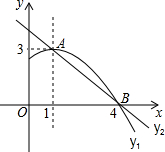 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: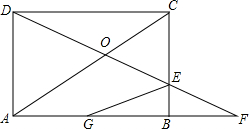 如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).
如图,已知矩形ABCD的边长AB=8cm,BC=6cm,动点G从点A从发沿AB方向以2m/s的速度向点B匀速运动;同时,动点E从点B出发沿BC方向以1m/s的速度向点C匀速运动,连接DE并延长交AB的延长线于点F,设运动时间为t秒(0<t<4).