题目内容
 如图:在等腰直角三角形ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,交AD于G.求证:(1)Rt△CBF≌Rt△ACD;
如图:在等腰直角三角形ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,交AD于G.求证:(1)Rt△CBF≌Rt△ACD;(2)AD⊥CF.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)先证出CD=DB,BF=DB,得出BF=CD,再证出∠CBF=∠ACD,由BC=AC,即可证出Rt△CBF≌Rt△ACD(SAS);
(2)由Rt△CBF≌Rt△ACD得出∠BCF=∠CAD,从而证出∠AGC=90°,得出AD⊥CF.
(2)由Rt△CBF≌Rt△ACD得出∠BCF=∠CAD,从而证出∠AGC=90°,得出AD⊥CF.
解答:证明:(1)∵△ABC是等腰直角三角形,
∴AC=CB,∠CBA=∠CAB=45°,
∵DE⊥AB,
∴∠DEB=90°,∠BDE=45°,
又∵BF∥AC∴∠CBF=90°,∴∠BFD=∠BDE=45°,∠BFD=∠ACD=90°,
∴BF=DB,
∵D为BC的中点,
∴CD=DB,
∴BF=CD,
在Rt△CBF和Rt△ACD中,
∴Rt△CBF≌Rt△ACD(SAS);
(2)由(1)得Rt△CBF≌Rt△ACD,
∴∠BCF=∠CAD,
∵∠BCF+∠GCA=90°,
∴∠CAD+∠GCA=90°,即∠AGC=90°,
∴AD⊥CF.
∴AC=CB,∠CBA=∠CAB=45°,
∵DE⊥AB,
∴∠DEB=90°,∠BDE=45°,
又∵BF∥AC∴∠CBF=90°,∴∠BFD=∠BDE=45°,∠BFD=∠ACD=90°,
∴BF=DB,
∵D为BC的中点,
∴CD=DB,
∴BF=CD,
在Rt△CBF和Rt△ACD中,
|
∴Rt△CBF≌Rt△ACD(SAS);
(2)由(1)得Rt△CBF≌Rt△ACD,
∴∠BCF=∠CAD,
∵∠BCF+∠GCA=90°,
∴∠CAD+∠GCA=90°,即∠AGC=90°,
∴AD⊥CF.
点评:本题考查了等腰直角三角形的性质和全等三角形的判定与性质;证明三角形全等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )
如图所示,D,E,F分别是△ABC三边的中点,G是AE的中点,BE与DF、DG分别交于P,Q两点,则PQ:BE=( )| A、1:2 | B、1:4 |
| C、1:6 | D、1:8 |
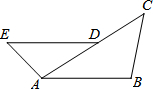 已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.
已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.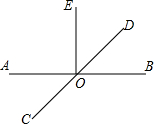 直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.
直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.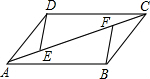 如图,AB=CD,BC=DA,E,F在AC上,且AE=CF.试说明:△BCF≌△DAE.
如图,AB=CD,BC=DA,E,F在AC上,且AE=CF.试说明:△BCF≌△DAE. 如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD=
如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD=