题目内容
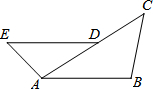已知：如图，D是AC上一点，DE∥AB，∠B=∠DAE．（1）求证：△ABC∽△DAE；
（2）若AB=8，AD=6，AE=4，求BC的长．
考点：相似三角形的判定与性质
专题：
分析：（1）由两直线平行，内错角相等，可得：∠EDA=∠CAB，由∠B=∠DAE，然后根据两角对应相等，两三角形相似，可证△ABC∽△DAE；
（2）由相似三角形对应边成比例，可得：
=
，然后将AB=8，AD=6，AE=4，代入即可．
（2）由相似三角形对应边成比例，可得：
| BC |
| AE |
| BA |
| AD |
解答：（1）证明：∵DE∥AB，
∴∠ADE=∠CAB，
∵∠B=∠DAE，
∴△ABC∽△DAE；
（2）∵△ABC∽△DAE，
∴
=
，
∵AB=8，AD=6，AE=4，
∴
=
．
∴BC=
．
∴∠ADE=∠CAB，
∵∠B=∠DAE，
∴△ABC∽△DAE；
（2）∵△ABC∽△DAE，
∴
| BC |
| AE |
| BA |
| AD |
∵AB=8，AD=6，AE=4，
∴
| BC |
| 4 |
| 8 |
| 6 |
∴BC=
| 16 |
| 3 |
点评：此题考查了相似三角形的判定与性质，关键知道两角对应相等两个三角形相似及相似三角形对应边成比例．
练习册系列答案
相关题目
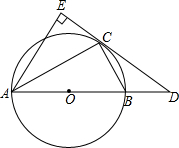如图，AB是⊙O的直径，D是AB的延长线上的一点，点C在⊙O上，AE⊥DC交
⊙O中，AB是直径，弦CD与AB交于E，AE=8，BE=2，∠AEC=30°，求CD的长．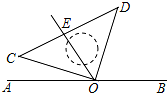
如图，一直角三角板COD的直角（∠COD=90°）顶点O落在直线AB上，射线OE平分∠AOD．
如图所示，在矩形ABCD中，DE⊥AC于点E，设∠ADE=a，且cosa=| 3 |
| 5 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
已知：如图，BD是△ABC的高，AB=6，AC=5下列四组数中不能构成直角三角形的一组是（ ）
A、1，2，
| ||||
B、
| ||||
| C、13，12，5 | ||||
D、1，3，
|
如图：在等腰直角三角形ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，交AD于G．求证：（1）Rt△CBF≌Rt△ACD；