题目内容
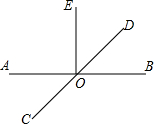 直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.
直线AB、CD相交于点O,∠AOC=45°,∠AOD=3∠DOE,图中的线是否存在互相垂直的关系?若存在,请写出互相垂直的线,并说明理由;若不存在,请直接说明理由.考点:垂线,对顶角、邻补角
专题:
分析:根据邻补角的定义,可得∠DOA,根据∠AOD=3∠DOE,可得∠DOE的度数,再根据角的和差,可得∠AOE的度数,可得答案.
解答:解:OE⊥AB,理由如下:
由角的和差,得∠AOD=180°-∠AOC=180°-45°=135°,
由∠AOD=3∠DOE=135°,得
∠DOE=45°,
由角的和差,得∠AOE=∠AOD-∠EOD=135°-45°=90°,
∴OE⊥AB.
由角的和差,得∠AOD=180°-∠AOC=180°-45°=135°,
由∠AOD=3∠DOE=135°,得
∠DOE=45°,
由角的和差,得∠AOE=∠AOD-∠EOD=135°-45°=90°,
∴OE⊥AB.
点评:本题考查了垂线,利用了邻补角的定义,角的和差.

练习册系列答案
相关题目
下列四组数中不能构成直角三角形的一组是( )
A、1,2,
| ||||
B、
| ||||
| C、13,12,5 | ||||
D、1,3,
|
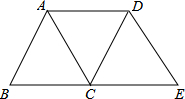 如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )| A、AB=BC |
| B、AC=BC |
| C、∠B=60° |
| D、∠ACB=60° |
 ⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长.
⊙O中,AB是直径,弦CD与AB交于E,AE=8,BE=2,∠AEC=30°,求CD的长. 如图,已知点O在直线CD上,当∠1和∠2满足条件
如图,已知点O在直线CD上,当∠1和∠2满足条件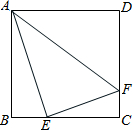 如图,在边长为a的正方形中,E、F分别为边BC和CD上的动点,当点E和点F运动时,AE和EF保持垂直.则:
如图,在边长为a的正方形中,E、F分别为边BC和CD上的动点,当点E和点F运动时,AE和EF保持垂直.则: 如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数
如图,以原点O为顶点的等腰直角三角形ABO中,∠BAO=90°,反比例函数 如图:在等腰直角三角形ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,交AD于G.求证:(1)Rt△CBF≌Rt△ACD;
如图:在等腰直角三角形ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,交AD于G.求证:(1)Rt△CBF≌Rt△ACD;