题目内容
4.(1)计算:$\sqrt{8}$+($\frac{1}{3}$)-1+|$\sqrt{2}$-2|-2cos45°(2)解不等式组$\left\{\begin{array}{l}{3x+1<x-3}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1}\end{array}\right.$.
分析 (1)原式第一项化为最简二次根式,第二项利用负整数指数幂法则计算,第三项利用绝对值的代数意义化简,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=2$\sqrt{2}$+3+2-$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$=5;
(2)$\left\{\begin{array}{l}{3x+1<x-3①}\\{\frac{1+x}{2}≤\frac{1+2x}{3}+1②}\end{array}\right.$,
由①得:x<-2,
由②得:x≥-5,
则不等式组的解集为-5≤x<-2.
点评 此题考查了实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.
如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.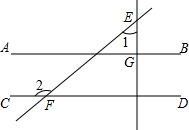 如图,已知直线AB∥CD,直线EG垂直于AB,垂足为G,直线EF交CD于点F,∠1=50°,则∠2=140°.
如图,已知直线AB∥CD,直线EG垂直于AB,垂足为G,直线EF交CD于点F,∠1=50°,则∠2=140°. 如图,菱形ABCD的对角线AC、BD的长分别是6,2$\sqrt{3}$,如果用一个2倍放大镜看菱形ABCD,则∠BAD=60°,菱形ABCD的周长=16$\sqrt{3}$,面积=24$\sqrt{3}$.
如图,菱形ABCD的对角线AC、BD的长分别是6,2$\sqrt{3}$,如果用一个2倍放大镜看菱形ABCD,则∠BAD=60°,菱形ABCD的周长=16$\sqrt{3}$,面积=24$\sqrt{3}$.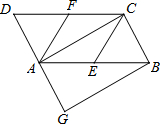 如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.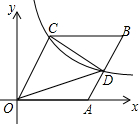 如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$).
如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$).