题目内容
14.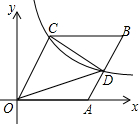 如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$).
如图,已知菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{4}{x}$(x>0)的图象恰好经过点C,且与AB交于点D,若△OCD的面积为2$\sqrt{2}$,则点B的坐标为($2\sqrt{2}+2,2$).
分析 根据题意可以分别设出点A、点C的坐标,根据菱形的性质和△OCD的面积为2$\sqrt{2}$,可以得到关于a、b的二元一次方程组,从而可以得到a、b的值,进而可以得到点C的坐标.
解答 解:由题意可得,设点A的坐标为(a,0),点C的坐标是(b,$\frac{4}{b}$),
∴$\left\{\begin{array}{l}{\frac{a•\frac{4}{b}}{2}=2\sqrt{2}}\\{a=\sqrt{{b}^{2}+(\frac{4}{b})^{2}}}\end{array}\right.$
解得,$\left\{\begin{array}{l}{a=2\sqrt{2}}\\{b=2}\end{array}\right.$
∴点A的坐标是(2$\sqrt{2}$,0),点C的坐标是(2,2),
∴点B的坐标是($2\sqrt{2}+2,2$).
故答案为:($2\sqrt{2}+2,2$).
点评 本题考查反比例函数系数k的几何意义、菱形的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
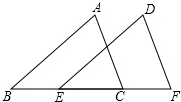 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.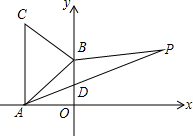 如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.
如图所示,A(-$\sqrt{3}$,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内.