题目内容
12.已知⊙O是半径为2的圆形纸板,现要在其内部设计一个内接正三角形图案,则内接正三角形的边长为2$\sqrt{3}$.分析 根据题意画出图形,欲求△ABC的边长,把△ABC中BC边当弦,作BC的垂线,在Rt△BOD中,求BD的长;根据垂径定理知:BC=2BD,从而求正三角形的边长即可.
解答 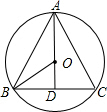 解:如图所示:
解:如图所示:
∵△ABC是等边三角形,⊙O的半径为2,
∴在Rt△BOD中,OB=2,∠OBD=30°,
∴BD=cos30°×OB=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$,
∵BD=CD,
∴BC=2BD=2$\sqrt{3}$,即它的内接正三角形的边长为2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查的是三角形的外接圆与外心,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
2.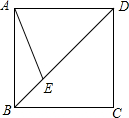 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | 4-2$\sqrt{2}$ |
3.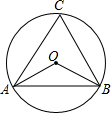 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
17.下列图形中,轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).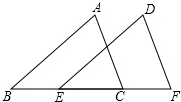 如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.
如图,B、E、C、F四点在同一直线上,AB∥DE,BE=CF,∠A=∠D,求证:AC=DF.